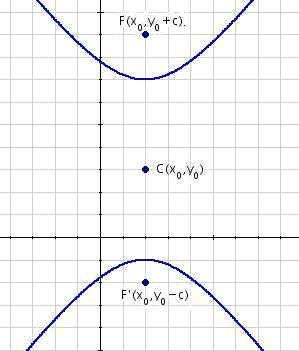
A continuació s'analitzen les hipèrboles verticals amb centre al punt genèric $$C(x_0,y_0)$$. L'eix focal és ara paral·lel a l'eix de les ordenades, i per tant els focus estan en els punts $$F'(x_0,y_0-c)$$ i $$F(x_0,y_0+c)$$.
Aplicant ara la definició general obtenim $$$\sqrt{(x-x_0)^2+(y-y_0+c)^2}-\sqrt{(x-x_0)^2+(y-y_0-c)^2}=2a$$$
Se suma l'arrel i s'eleva al quadrat: $$$\begin{array}{rcl} \Big(\sqrt{(x-x_0)^2+(y-y_0+c)^2}\Big)^2 & = & \Big( 2a+\sqrt{(x-x_0)^2+(y-y_0-c)^2} \Big)^2 \\ (x-x_0)^2+(y-y_0+c)^2 & = & 4a^2+4a \sqrt{(x-x_0)^2+(y-y_0-c)^2}+ \\ & & +(x-x_0)^2+(y-y_0-c)^2 \\ (x-x_0)^2+(y-y_0)^2+2(y-y_0)c+c^2 & = & 4a^2+4a \sqrt{(x-x_0)^2+(y-y_0-c)^2}+ \\ & & +(x-x_0)^2+(y-y_0)^2-2(y-y_0)^2 \\ & & -2(y-y_0)c+c^2\end{array}$$$
Al simplificar i dividint entre quatre: $$$\begin{array}{rcl} 4(y-y_0)c & = & 4a^2+4a\sqrt{(x-x_0)^2+(y-y_0-c)^2} \\ (y-y_0)c & = & a^2+a \sqrt{(x-x_0)^2+(y-y_0-c)^2} \end{array}$$$
En aïllar l'arrel i elevar novament al quadrat: $$$\begin{array}{rcl} (c(y-y_0)-a^2)^2 & = & \Big(a\sqrt{(x-x_0)^2+(y-y_0-c)^2}\Big)^2 \\ c^2(y-y_0)^2-2a^2c(y-y_0)+a^4 & = & a^2((x-x_0)^2+(y-y_0-c)^2) \\ c^2(y-y_0)^2-2a^2c(y-y_0)+a^4 & = & a^2 ((x-x_0)^2+(y-y_0)^2-2c(y-y_0)+c^2) \\ c^2(y-y_0)^2-2a^2c(y-y_0)+a^4 & = & a^2(x-x_0)^2+a^2(y-y_0)^2-2a^2c(y-y_0)+a^2c^2 \\ c^2(y-y_0)^2-a^2(y-y_0)^2-a^2(x-x_0)^2& = & a^2 c^2-a^4 \\ (c^2-a^2)(y-y_0)^2-a^2(x-x_0)^2 & = & a^2(c^2-a^2) \end{array}$$$
Dividir llavors entre $$a^2(c^2-a^2)$$ per obtenir un $$1$$ a la dreta: $$$\displaystyle \begin{array}{rcl} \frac{(c^2-a^2)(y-y_0)^2}{a^2(c^2-a^2)}-\frac{a^2(x-x_0)^2}{a^2(c^2-a^2)} & = & 1 \\ \frac{(y-y_0)^2}{a^2}-\frac{(x-x_0)^2}{(c^2-a^2)}=1 \end{array}$$$
En aplicar la definició $$c^2=a^2+b^2=$$, $$b^2= c^2-a^2$$ es substitueix i s'arriba a l'equació desitjada per a la hipèrbola vertical: $$$\displaystyle \frac{(y-y_0)^2}{a^2}-\frac{(x-x_0)^2}{b^2}=1$$$
A continuació es veurà un exemple pràctic en el qual s'observarà de forma més senzilla els passos realitzats per arribar a l'equació per a la hipèrbola vertical.
Trobeu l'equació de la hipèrbola els focus estan en els punts $$F' (3,-1)$$ i $$F (3,5)$$ i excentricitat $$\displaystyle e=\frac{3}{2}$$.
Identificant en $$F'(x_0,y_0-c)$$ i en $$F(x_0,y_0+c)$$, es troba $$x_0=3, \ y_0= 2$$ i $$c=3$$.
Aplicant la fórmula per l'excentricitat $$\displaystyle e=\frac{c}{a}$$ s'aïlla $$a=2$$.
Aplicant ara $$\overline{PF}-\overline{PF'}=2a$$ obtenim $$$\displaystyle \sqrt{(x-3)^2+(y-2+3)^2}-\sqrt{(x-3)^2+(y-2-3)^2}= 2 \cdot 2$$$ Tal com es va fer teòricament, se suma l'arrel i s'eleva al quadrat: $$$\displaystyle \begin{array}{rcl} \Big( \sqrt{(x-3)^2+(y-2+3)^2}\Big) ^2 & = & \Big( 4+\sqrt{(x-3)^2+(y-2-3)^2}^2 \\ (x-3)^2+(y-2+3)^2 & = & 4^2+4 \cdot 2 \sqrt{(x-3)^2+(y-2-3)^2} \\ & & +(x-3)^2+(y-2-3)^2 \\ (x-3)^2+(y-2)^2+2 \cdot 3 (y-2) + 3^3 & = & 16+8\sqrt{(x-3)^2+(y-2-3)^2}+ \\ & & +(x-3)^2+(y-2)^2-2 \cdot 3 (y-2) \\ & & +3^2 \end{array} $$$ Al simplificar i dividint llavors per quatre: $$$\begin{array} {rcl} 12(y-2) & = & 16+8\sqrt{(x-3)^2+(y-2-3)^2} \\ 3(y-2) & = & 4+2\sqrt{(x-3)^2+(y-2-3)^2} \end{array}$$$ En aïllar l'arrel i elevar novament al quadrat: $$$\begin{array} {rcl} \Big(3(y-2)-4\Big)^2 & = & \Big(2\sqrt{(x-3)^2+(y-2-3)^2}\Big) \\ 3^2(y-2)^2-2 \cdot 3 \cdot 4 (y-2) + 4^2 & = & 2^2((x-3)^2+(y-2-3)^2) \\ 9(y-a)^2-24 (y-2) + 16 & = & 4((x-3)^2+(y-2)^2-2 \cdot 3 (y-2)+3^2) \\ 9(y-2)^2-24(y-2)+16 & = & 4(x-3)^2+4(y-2)^2-24(y-2)+36 \\ 9(y-2)^2-4(y-2)^2-4(x-3)^2 & = & 36-16 \\ (9-4)(y-2)^2-4(x-3)^2 & = & 20 \\ 5(y-2)^2-4(x-3)^2 & = & 20\end{array}$$$ Al dividir llavors entre $$20$$ per obtenir un $$1$$ a la dreta: $$$ \displaystyle \begin{array}{rcl} \frac{5(y-2)^2}{20}-\frac{4(x-3)^2}{20} & = & 1 \\ \frac{(y-2)^2}{4}- \frac{(x-3)^2}{5}=1 \end{array}$$$ i es troba l'equació desitjada.
En desenvolupar l'equació tant de la hipèrbola vertical com de l'horitzontal, en general, es pot expressar l'equació de la forma $$Ax^2+By^2+Cx+Dy+E=0$$ on $$A$$ i $$B$$ no poden tenir el mateix signe.
Transformar l'equació de l'exercici anterior a la forma $$Ax^2+By^2+Cx+Dy+E=0$$.
Partint de $$\displaystyle \frac{(y-2)^2}{4}-\frac{(x-3)^2}{5}=1$$ es multiplica pel $$m.c.m (4,5)$$: $$$5(y-2)^2-4(4x-3)^2= 20$$$ Seguidament es desenvolupen els quadrats i es deixa tot a un mateix costat de l'equació: $$$\begin{array}{rcl} 5(y^2-2 \cdot 2y +2^2)-4(x^2-2 \cdot 3x+3^2 ) & = & 20 \\ 5y^2-5 \cdot 4y+ 5 \cdot 4-4x^2+4 \cdot 6x-4 \cdot 9 -20 & = & 0 \\ 5y^2-20y+20-4x^2+24x-36-20 & = & 0 \\ -4x^2+5y^2+24x-20y-36 & = & 0 \end{array}$$$