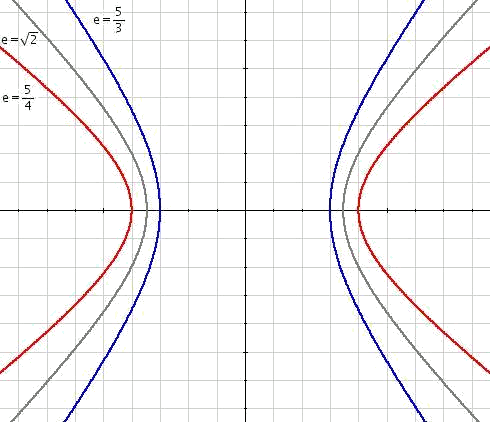
Una hipèrbola és la corba formada pel conjunt de punts del pla la diferència de distàncies a dos punts fixos, els focus, és constant: $$\overline{PF}- \overline {PF'}=2a$$
- Focus: Són els dos punts fixos $$F$$ i $$F'$$.
- Eix focal: És l'eix creat per la recta $$FF'$$ i la longitud és la distància focal.
- Distància focal o real: Distància del segment $$\overline{FF'}=2c$$.
- Eix secundari o imaginari: Eix format pel conjunt de punts equidistants de $$F$$ i $$F'$$. És per tant la mediatriu del segment $$\overline{FF'}$$.
- Centre: És el punt mig del segment $$\overline{FF'}$$. També és el punt on es creuen l'eix focal i l'eix secundari.
- Eixos de simetria: Tant l'eix focal com l'eix secundari són eixos de simetria.
- Vèrtexs: Els vèrtexs $$A$$ i $$A'$$ són els punts d'intersecció de l'eix focal amb la hipèrbola.
- Els vèrtexs $$B$$ i $$B'$$ s'obtenen de les interseccions de l'eix secundari amb el cercle de centre $$A$$ i de radi $$c$$.
- Per simetria també es troben amb el cercle de centre $$A'$$ i del mateix radi.
- Eix major: És l'eix creat pel segment $$\overline{AA'}$$ i de longitud $$2a$$.
- Eix menor: És l'eix creat pel segment $$\overline{BB'}$$ i de longitud $$2b$$.
- Relació entre semieixos: $$c^2=a^2+b^2$$.
- Radis vectors: Són els segments $$PF$$ i $$PF'$$, que uneixen els focus amb un punt de la hipèrbola.
- Asímptotes: Una hipèrbola té dues asímptotes d'equacions respectives $$\displaystyle y=\frac{b}{a}x$$ i $$\displaystyle y=-\frac{b}{a}x$$.
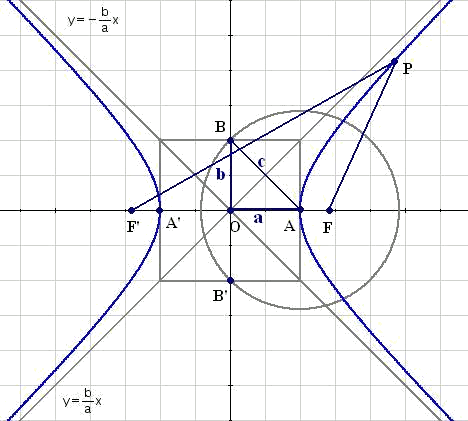
Excentricitat
L'excentricitat ens dóna informació sobre l'obertura de les branques de la hipèrbola. $$$\displaystyle e=\frac{c}{a}$$$ Com $$c\geq a$$, dividint a banda i banda per $$a$$: $$\displaystyle \frac{c}{a} \geq 1$$.
S'identifica llavors l'excentricitat $$e \geq 1$$.
En el cas límit $$e=1$$ les branques són horitzontals. A mesura que l'excentricitat augmenta cada vegada són més verticals les branques de la hipèrbola com es veu amb $$\displaystyle e=\frac{5}{4}, e=\sqrt{2}$$ (Hipèrbola equilàtera) i $$\displaystyle e=\frac{5}{3}$$.
