A hyperbola is the curve formed by the set of points of the plane, for which the difference of distances to two fixed points, the foci, is constant: $$\overline{PF}- \overline {PF'}=2a$$
- Foci: There are two fixed points $$F$$ and $$F'$$.
- Focal axis: It is the axis created by the straight line $$FF'$$ and whose length is the focal distance.
- Focal or real distance: It is the distance of the segment $$\overline{FF'}=2c$$.
- Secondary or imaginary axis: Axis formed by the set of equidistant points of $$F$$ and $$F'$$. It is therefore the perpendicular bisector of the segment $$\overline{FF'}$$.
- Center: It is the average point of the segment $$\overline{FF'}$$. Also, it is the point where the focal axis and the secondary axis intersect.
- Symmetry axes: Both the focal axis and the secondary axis are symmetry axes.
- Apexes: The apexes $$A$$ and $$A'$$ are the points of intersection of the focal axis with the hyperbola.
- The apexes $$B$$ and $$B'$$ are obtained with the intersections of the secondary axis with the center circle $$A$$ and of radius $$c$$.
- For symmetry they are found with the center circle $$A'$$ and with the same radius.
- Major axis: It is the axis created by the segment $$\overline{AA'}$$ and of length $$2a$$.
- Less axis: It is the axis created by the segment $$\overline{BB'}$$ and of length $$2b$$.
- Relation between semiaxes: $$c^2=a^2+b^2$$.
- Radioes vectors: The segments $$PF$$ and $$PF'$$, that join the foci with a point of the hyperbola.
- Asymptotes: A hyperbola has two asymptotes of respective equations $$\displaystyle y=\frac{b}{a}x$$ and $$\displaystyle y=-\frac{b}{a}x$$.
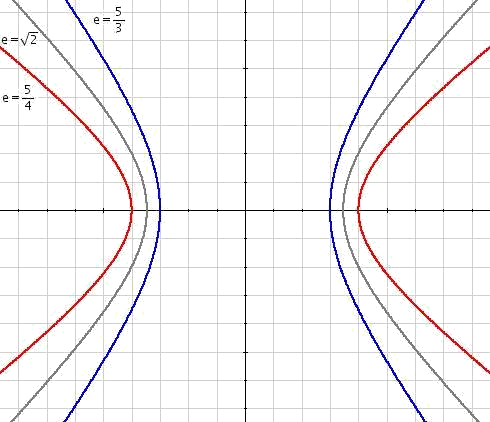
Eccentricity
The eccentricity gives us information about the gap in the branches of the hyperbola. $$$\displaystyle e=\frac{c}{a}$$$ As $$c\geq a$$, dividing on both sides for $$a$$: $$\displaystyle \frac{c}{a} \geq 1$$.
The eccentricity is identified then $$e \geq 1$$.
In the extreme case $$e=1$$ the branches are horizontal. As the eccentricity increases more and more the branches of the hyperbola are more vertical as one sees with $$\displaystyle e=\frac{5}{4}, e=\sqrt{2}$$ (equilateral hyperbola) and $$\displaystyle e=\frac{5}{3}$$.
