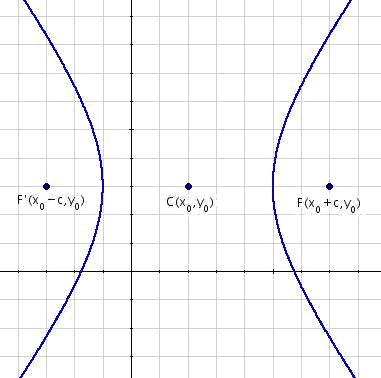
En aquest apartat es tractaran les hipèrboles horitzontals amb el centre en un punt genèric $$C(x_0,y_0)$$.
L'eix focal és paral·lel a l'eix d'abscisses, i per tant els focus estan en les coordenades $$F'(x_0-c,y_0)$$ i $$F(x_0+c,y_0)$$.
Aplicant aquests focus en la definició general de la hipèrbola $$\overline{PF}- \overline {PF'}=2a$$ s'obté l'expressió $$$\sqrt{(x-x_0+c)^2+(y-y_0)^2}-\sqrt{(x-x_0-c)^2+(y-y_0)^2}=2a$$$
Al sumar l'arrel, i elevant al quadrat: $$$\begin{array}{rcl} \Big(\sqrt{(x-x_0+c)^2+(y-y_0)^2}\Big)^2 & = & \Big(2a+\sqrt{(x-x_0-c)^2+(y-y_0)^2}\Big)^2 \\ (x-x_0+c)^2+(y-y_0)^2 & = & 4a^2+4a\sqrt{(x-x_0-c)^2+(y-y_0)^2}+ \\ & & +(x-x_0-c)^2+(y-y_0)^2 \\ (x-x_0)^2+2(x-x_0)c+c^2+(y-y_0)^2 & = & 4a^2+4a\sqrt{(x-x_0-c)^2+(y-y_0)^2}+ \\ & & +(x-x_0)^2-2(x-x_0)c+c^2+(y-y_0)^2\end{array}$$$
Simplificant i dividint per quatre: $$$\begin{array}{rcl} 4(x-x_0)c & = & 4a^2+4a \sqrt{(x-x_0-c)^2+(y-y_0)^2} \\ (x-x_0)c & = & a^2+a\sqrt{(x-x_0-c)^2+(y-y_0)^2}\end{array}$$$
En aïllar l'arrel i elevar novament al quadrat: $$$\begin{array}{rcl} (c(x-x_0)-a^2)^2 & = & (a\sqrt{(x-x_0-c)^2+(y-y_0)^2})^2 \\ c^2(x-x_0)^2-2a^2c(x-x_0)+a^4& = & a^2((x-x_0)^2+(y-y_0)^2 \\ c^2(x-x_0)^2-2a^2c(x-x_0)+a^4& = & a^2((x-x_0)^2-2c(x-x_0)+x^2+(y-y_0)^2) \\ c^2(x-x_0)^2-2a^2c(x-x_0)+a^4 & = & a^2(x-x_0)^2-2ac(x-x_0)+a^2c^2+a^2(y-y_0)^2\\ c^2(x-x_0)^2 -a^2(x-x_0)^2-a^2(y-y_0)^2 & = & a^2c^2-a^4 \\ (c^2-a ^2)(x-x_0)^2-a^2(y-y_0)^2& = &a^2(c^2-a^2) \end{array}$$$
Es divideix llavors per $$a^2(c^2-a^2)$$ per obtenir un $$1$$ a la dreta: $$$\begin{array}{rcl} \dfrac{(c^2-a ^2)(x-x_0)^2}{a^2(c^2-a^2)}-\dfrac{a^2(y-y_0)^2}{a^2(c^2-a^2)}& = &1 \\ \dfrac{(x-x_0)^2}{a^2}-\dfrac{(y-y_0)^2}{(c^2-a^2)}& = &1 \end{array}$$$
Aplicant la definició $$c^2=a^2+b^2$$, $$b^2=c^2-a^2$$ es substitueix i s'arriba a l'equació desitjada: $$$\displaystyle \frac{(x-x_0)^2}{a^2}-\frac{(y-y_0)^2}{b^2}= 1$$$
Trobeu l'equació de la hipèrbola de centre $$C (2,3)$$, vèrtex $$A (2,6)$$ i de focus $$F (2,7)$$.
La distància focal $$$c=7-3=4 \\ a=6-3=3$$$ Amb $$c^2=a^2+b^2$$, so $$b=\sqrt{c^2-a^2}=\sqrt{16-9}=\sqrt{7}$$.
Substituint a $$$\displaystyle \frac{(x-x_0^2)}{a^2}-\frac{(y-y_0)^2}{b^2}=1$$$ i identificant $$C(x_0,y_0)$$, resulta $$$\displaystyle \frac{(x-2)^2}{9}-\frac{(y-3)^2}{7}= 1$$$