Euclidian distance

Euclidian distance

The absolute value allows to define the distance between two real numbers.

Given two numbers $a$ and $b$, they determine two points on the real line, which we denote by $A$ and $B$. We define the distance between $a$ and $b$ as the length of the segment $AB$.

Let's see the different cases that we can find:

1. $0<a<b$: in this case, both numbers are on the right of zero. Then, the length of the segment is calculated doing: $$AB=0B-0A=b-a=|b-a|$$

As we can see in the figure:

2. $a<b<0$: in this case, both numbers are on the left of zero. Then, the length of the segment is calculated by doing $$AB=0A-0B=-a-(-b)=a-b=-(b-a)=|b-a|$$ Graphically:

3. $a<0<b$: in this case we have one number on the right and another on the left of zero. In this case we have that the length of the segment is $$AB=A0+0B=-a+b=-(b-a)=|b-a|$$ Or graphically:

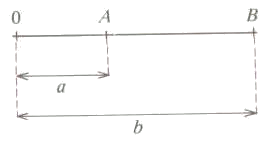
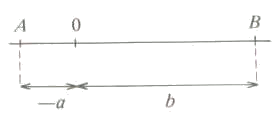
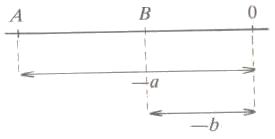
In general, we can say that the distance between two numbers $a$ and $b$, is the absolute value of its difference, and we will denote it by: $$d(a,b)=|b-a|$$

Properties of the Euclidian distance

As consequences of the properties of the absolute value we see that, considering three real numbers $a,b$ and $c$, it is satisfied that

• $d(a,b)>0$; and $d(a,b)=0$ if and only if $a=b$.
• $d(a,b)=d(b,a)$.
• $d(a,b)\le d(a,c)+d(c,b)$

The absolute value and the distance defined previously are named as Euclidean norm and Euclidean distance, respectively. These represent the most intuitive distance concept on the real line.