Distància euclidiana
El valor absolut permet definir la distància entre dos nombres reals.
Donats dos nombres $$a$$ i $$b$$, determinen dos punts sobre la recta real, que anomenem $$A$$ i $$B$$. Definim la distància entre $$a$$ i $$b$$ com la longitud del segment $$AB$$.
Vegem els diferents casos que es poden donar:
- $$0 < a < b$$: en aquest cas, ambdós números es troben a la dreta del zero. Llavors, la longitud del segment es calcula fent: $$$AB=0B-0A=b-a=|b-a|$$$
Com podem veure a la figura:
- $$a < b < 0$$: en aquest cas, ambdós números es troben a l'esquerra del zero. Llavors, la longitud del segment es calcula fent $$$AB=0A-0B=-a-(-b)=a-b=-(b-a)=|b-a|$$$ Gràficament:
- $$a < 0 < b$$: en aquest cas tenim un nombre a la dreta i un altre a l'esquerra del zero. En aquest cas la longitud del segment ens queda $$$AB=A0+0B=-a+b=-(b-a)=|b-a|$$$ O gràficament:
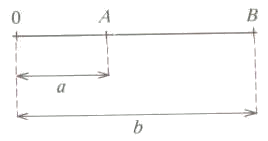
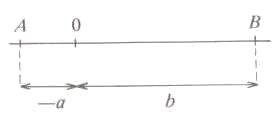
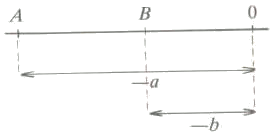
En general, podem dir que la distància entre dos nombres $$a$$ i $$b$$, és el valor absolut de la seva diferència, i el denotarem amb: $$$d(a,b)=|b-a|$$$
Propietats de la distància euclidiana
Com a conseqüències de les propietats del valor absolut tenim que, donats dos nombres reals $$a,b$$ i $$c$$, es compleix
- $$d(a,b)>0$$; i $$d(a,b)=0$$ si i només si $$a=b$$.
- $$d(a,b)=d(b,a)$$.
- $$d(a,b) \leq d(a,c) + d(c,b)$$
$$d(3,-2)=|-2-3| = |-5|=5$$
$$d(-7,-1)=|-1-(-7)| = |-1+7|=6$$
El valor absolut i la distància definits anteriorment s'anomenen norma euclidianes i distància euclidiana, respectivament. Aquestes representen el concepte més intuïtiu de distància sobre la recta real.