Distancia euclídea
El valor absoluto permite definir la distancia entre dos números reales.
Dados dos números $$a$$ y $$b$$, determinan dos puntos sobre la recta real, que denotamos por $$A$$ y $$B$$. Definimos la distancia entre $$a$$ y $$b$$ como la longitud del segmento $$AB$$.
Veamos los distintos casos que se pueden dar:
- $$0 < a < b$$: en este caso, ambos números se encuentran a la derecha del cero. Entonces, la longitud del segmento se calcula haciendo $$$AB=0B-0A=b-a=|b-a|$$$
Como podemos ver en la figura:
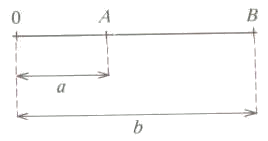
- $$a < b < 0$$: en este caso, ambos números se encuentran a la izquierda del cero. Entonces, la longitud del segmento se calcula haciendo $$$AB=0A-0B=-a-(-b)=a-b=-(b-a)=|b-a|$$$ Gráficamente:
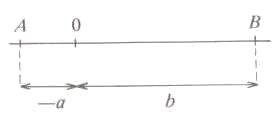
- $$a < 0 < b$$: en este caso tenemos un número a la derecha y otro a la izquierda del cero. En este caso la longitud del segmento nos queda $$$AB=A0+0B=-a+b=-(b-a)=|b-a|$$$ O gráficamente:
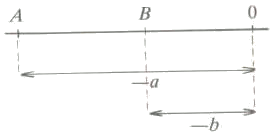
En general, podemos decir que la distancia entre dos números $$a$$ y $$b$$, es el valor absoluto de su diferencia, y lo denotaremos con: $$$d(a,b)=|b-a|$$$
Propiedades de la distancia euclídea
Como consecuencias de las propiedades del valor absoluto tenemos que, dados tres números reales $$a,b$$ y $$c$$, se cumple
- $$d(a,b)>0$$; y $$d(a,b)=0$$ si y solo si $$a=b$$.
- $$d(a,b)=d(b,a)$$.
- $$d(a,b) \leq d(a,c) + d(c,b)$$
$$d(3,-2)=|-2-3| = |-5|=5$$
$$d(-7,-1)=|-1-(-7)| = |-1+7|=6$$
El valor absoluto y la distancia definidos anteriormente se denominan norma euclídeas y distancia euclídea, respectivamente. Estas representan el concepto más intuitivo de distancia sobre la recta real.
