Express and operate with time in hours, minutes and seconds

Expressing time in hours, minutes and seconds

Let's observe a clock:

imagen

As we can see, this is a circumference. The big hand and th little hand are constantly forming angles since they have a common point (the center of the clock), which is also the center of the circumference.

Given a circumference we can choose that a full rotation of the big hand can be called either $360^{\circ}$ or $2 π$ radians. Now we will take degrees as a measurement. So, a full rotation is $360^{\circ}$ . At the same time, this corresponds to an hour on the clock face. And so, a full rotation, being $360^{\circ}$ , can also be understood as an hour.

Once we have established this measurement of time, let's see how to work with it. To express quantities of time that do not correspond to an exact number of hours we use as a submultiple the sixtieth part of an hour, which is called a minute and is written as $^{'}$ , and the sixtieth part of a minute, which is called a second and is written as $^{″}$ . This means that $1 h = 60^{'}$ and $1^{'} = 60^{″}$ .

That is to say: $1 hour = 60 minutes = 60^{'}$

$1 minute = 60 seconds = 60^{″}$

So, if we want to express one hour in seconds we need to do conversion factors:

$1 hour = 60 minutes = 60 minutes \cdot \frac{60 seconds}{1 minute} =$ $= 60 \cdot 60 seconds = 3600 seconds$

For example,

Example

Let's express several values in minutes and seconds:

$4$ hours in minutes is: $4 hours = 4 hours \cdot \frac{60 minutes}{1 hour} = 4 \cdot 60 minutes = 240 minutes$

Half an hour in seconds: $\frac{1}{2} hour = \frac{1}{2} hour \cdot \frac{60 minutes}{1 hour} \frac{60 seconds}{1 minute} =$ $= \frac{60 \cdot 60}{2} seconds = 1800 seconds$

Example

When we have one minute and half, for example, we will write $1$ minute and its half, which is $30$ seconds, that is to say: $1^{'} 30^{″}$ .

If we want to write $7$ hours and a half, we will write $7$ and the half hour in minutes. Knowing that an hour is $60$ minutes, half an hour would be half of $60$ minutes, that is $30$ .

In this way, seven hours and a half are $7 h 30^{'}$ .

Example

We can also do it the other way around, that is to say, given any number of seconds, we can calculate how many minutes or hours they are.

For example: how many minutes are $1020$ seconds? $1020 seconds = 1020 seconds \cdot \frac{1 minute}{60 seconds} = \frac{1020}{60} minutes = 17 minutes$

Let's see what to do when the result is not an integer.

Example

Namely, let's suppose that we have $68$ seconds.

From now on we will use the standard minutes $^{'}$ and seconds $^{″}$ notation to speed up our writing and also to get used to it. Using conversion factors we have:

$68^{″} = 68^{″} \cdot \frac{1^{'}}{60^{″}} = \frac{68^{'}}{60} = 1, 13333^{'}$

But expressing $68^{″}$ as a decimal number of minutes is not so useful. We want to express it in a better way. For example, as $68^{″} = 60^{″} + 8^{″} = 1^{'} 8^{″}$ that is one minute and eight seconds.

To do this, we have to take the entire part of the result, multiply it by $60$ and subtract it from the original quantity.

That is:

In the previous case the result was $1, 13333$ , so we take the entire part, that is $1$ .

We multiply it by $60$ and the result is $60$ .

Now we subtract this $60$ from the original quantity that was $68$ .

The result is $8$ .

Therefore we have $1^{'} 8^{″}$ .

We will express the result as the entire part plus the difference.

Example

Let's suppose that we have $24355$ seconds. Let's express it in hours, minutes and seconds:

First we convert it into minutes:

$24355^{″} = 24355^{″} \cdot \frac{1^{'}}{60^{″}} = \frac{24355^{'}}{60} = {405.9166}^{'}$

Then we take the entire part of the above division, $405$ , and we multiply it by $60$ : $405 \cdot 60 = 24300$

Now, we subtract this number from the original quantity, obtaining: $24355 - 24300 = 55$

And so, we have that $24355^{″} = 405^{'} 55^{″}$

Now we must express $405^{'}$ in hours:

By means of the conversion factor: $405^{'} = 405^{'} \cdot \frac{1 h}{60^{'}} = \frac{405^{'}}{60} = 6.75 h$

We do the process again. We take the entire part, which is $6$ . We multiply it by $60$ and obtain $6 \cdot 60 = 360$ . We subtract this from the original quantity: $405^{'} - 360^{'} = 45$ ' And so, $405^{'} = 6 h 45^{'}$ Therefore, $24355^{″} = 6 h 45^{'} 55^{″}$

Once we can express quantities in hours, minutes and seconds, we will learn how to do operations between them.

Operations with time in hours, minutes and seconds

Addition

First, it is advisable to arrange them, seconds with seconds, minutes with minutes, hours with hours.

As we know, every minute has $60$ seconds, so, when adding seconds, we will have:

$15 seconds + 10 seconds = 25 seconds$ $30 seconds + 15 seconds = 45 seconds$

But

$30 seconds + 45 seconds = 75 seconds$

In this case, we know that $60 seconds = 1 minute$ , if we apply that to our previous example we have: $75 seconds = 60 seconds + 15 seconds$

In other words, $75 seconds = 1 minute$ and $15 seconds$

Now, if the number is very high, for example $1200$ seconds, the best thing to do is to divide this number by $60$ to obtain the minutes it represents. That is to say:

$\frac{1200}{60} = 20$

In other words, $1200 seconds = 20 minutes$ .

The same applies for the relation between minutes and hours. Every hour consists of $60 minutes$ .

If we have $45 minutes + 25 minutes = 70 minutes$ , it is the same as:

$70 minutes = 60 minutes + 10 minutes = 1 hour and 10 minutes$

Now let's see an example where there are decimals in the result.

Example

How many mminutes are $750$ seconds?

Well, let's take $750$ and let's divide it by $60$ $\frac{750}{60} = 12.5$

$750 = 12 minutes + 0.5 minutes$

Now, the easiest way to find out how many seconds this $0.5$ respresents is to multiply it by $60$ ( $0.5$ is expressed in minutes and now we need it in seconds)

$0.5 \cdot 60 = 30$ seconds. This is the procedure we have explained before.

Finally we have :

$750$ seconds $= 12$ minutes and $30$ seconds.

Example

$\begin{array}{ccccc} α & = & 74 h & 16^{'} & 54^{″} \\ β & = & 28 h & 45^{'} & 13^{″} \end{array}$ $α + β = (74 h 16^{'} 54^{″}) + (28 h 45^{'} 13^{″}) = 102 h 61^{'} 67^{″}$

In this way, we realize that what we need to do after adding the quantities is to check if the seconds exceed $60$ and, if so, express them in minutes and add them to those that we already have. And the same applies with minutes, if they exceed $60$ we will also have to convert them into hours.

In the previous case we had $67^{″}$ which is $1^{'} 7^{″}$ . Therefore, we rewrite the result adding one minute and leaving $7$ seconds. $103 h 62^{'} 7^{″}$

But now, since we have more than $60$ minutes, we add one more hour and we leave $2$ minutes (since we have $62^{'}$ ). Therefore: $103 h 2^{'} 7^{″}$ is the sum of those two quantities.

As a consequence of this, we already know how to add expressions given in hours, minutes and seconds. It is as simple as adding the differen quantities respectively (hours with hours, minutes with minutes, seconds with seconds) and then write the result while making sure that in the seconds there is always a number less than $60$ , and likewise in the minutes there is a number less than $60$ .

Subtraction

How will it work with subtraction?

We will proceed the same way: we will subtract the number of every unit from that of its corresponding unit. The only problem we can find is:

If the quantity of seconds to subtract is larger than the original quantity, what we have to do is:
- Subtract one minute from the original minutes quantity.
- To increase the original seconds quantity by $60$ .
Then we will proceed to subtract each quantity.

Example

$4^{'} 11^{″} - 2^{'} 47^{″}$ Since $11$ is less than $47$ , we subtract one minute from $4$ and add $60$ seconds to $11$ . The subtraction will look like this: $3^{'} 71^{″} - 2^{'} 47^{″} = 1^{'} 24^{″}$

Let's see another example that includes hours as well:

Example

$4 h 23^{'} 11^{″} - 2 h 47^{'} 27^{″}$

In this case $27$ is greater than $11$ , therefore we subtract one minute from the $23$ that we had and we add $60$ seconds to the 11 that we had. Now the subtraction is: $4 h 22^{'} 71^{″} - 2 h 47^{'} 27^{″}$

But now, we realize that in the minutes the same thing happens again, i.e., $47$ is bigger than $22$ minutes (in the original), therefore we subtract $1$ hour to the original and we add $60$ minutes. The subtraction now is:

$3 h 82^{'} 71^{″} - 2 h 47^{'} 27^{″} = 1 h 35^{'} 44^{″}$

Multiplication

Let's learn how to multiply one number expressed in hours, minutes and seconds by a natural number.

The procedure will be to multiply each of the factors (the seconds, the minutes and the hours) by the natural number and then to rewrite the result in the correct way, that is to say, keeping the digits of seconds and minutes under "60".

Example

$\frac{\begin{array}{ccc} 3 h & 12^{'} & 45^{″} \\ \times & 3 \end{array}}{\begin{array}{ccc} 9 h & 36^{'} & 135^{″} \end{array}}$

We convert the $135^{″}$ into minutes: $\frac{135}{60} = 2, 25$ We take the integer part, multiply it by $60$ and subtract it from $135$ , that is to say:

$135 - 2 \cdot 60 = 135 - 120 = 15$

Now we must add $2$ minutes to the $36$ that we already had and leave $15^{″}$ .

Therefore the result is: $9 h 38^{'} 15^{″}$ .

Division

In this section we will learn how to divide one number expressed in hours, minutes and seconds by a natural number.

To divide time by a natural number:

We divide the hours by the natural number and the remainder is multiplied by $60$ to convert it into minutes. Those minutes are then added to the dividend.
We divide the minutes by the natural number and the remainder is multiplied by $60$ to convert it into seconds. Those seconds are then added to the dividend.
Then we divide the seconds by the number.

Example

The following example allows us to make the division of $34 h 28^{'} 44^{″}$ by $4$ .

Step 1 We divide the hours by $4$ . $34 = 4 \cdot 8 + 2$

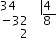
imagen

The remainder is $2$ , therefore we multiply it by $60$ and we add it to the minutes. $60 \cdot 2 = 120$ We add them to $28$ , $120 + 28 = 148^{'}$

Step 2 We divide the minutes by $4$ .

$148 = 4 \cdot 37 + 0$

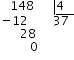
imagen

The remainder is $0$ , therefore there is no need to add anything to the seconds.

Step 3 We divide the seconds by $4$ . $44 = 4 \cdot 11 + 0$

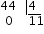
imagen

Finally, we write the result: $8 h 37^{'} 11^{″}$