Expressar i operar amb temps en hores, minuts i segons

Expressar temps en hores, minuts i segons

Observem ara un rellotge:

imagen

Com podem veure el rellotge és una circumferència. Les dues agulles que ens marquen les hores (el minuter i la de l'hora) estan constantment fent formes anguloses, ja que tenen un punt en comú, que a més coincideix amb el centre de la circumferència.

Donada una circumferència podem escollir que una volta sencera sigui anomenada amb $360^{\circ}$ o $2 π$ radiants. En aquest cas, prendrem com a mesura els graus. Així doncs, una volta sencera són $360^{\circ}$ . Però que al mateix temps correspon a una hora de rellotge. Així doncs, una volta sencera que eren $360^{\circ}$ , també pot ser entesa com una hora del rellotge.

Un cop establerta aquesta mesura del temps, veiem com es treballa amb ella. Per expressar quantitats de temps que no corresponen a un nombre exacte d'hores s'utilitzen com submúltiples la seixantena part d'una hora, que es diu minut i s'escriu amb $^{'}$ , i la seixantena part d'un minut, que es diu segon i s'escriu $^{″}$ . Això vol dir que $1 h = 60^{'}$ i $1^{'} = 60^{″}$ .

És a dir: $1 hora = 60 minuts = 60^{'}$

$1 minut = 60 segons = 60^{″}$

Si volem, doncs, expressar una hora en segons cal fer factors de conversió, és a dir escriure els canvis com

$1 hora = 60 minuts = 60 minuts \cdot \frac{60 segons}{1 minut} =$ $= 60 \cdot 60 segons = 3600 segons$

Exemple

Expressem diversos valors en minuts i segons:

$4$ hores en minuts és: $4 hores = 4 hores \cdot \frac{60 minuts}{1 hora} = 4 \cdot 60 minuts = 240 minuts$

Mitja hora en segons: $\frac{1}{2} hora = \frac{1}{2} hora \cdot \frac{60 minuts}{1 hora} \frac{60 segons}{1 minut} =$ $= \frac{60 \cdot 60}{2} segons = 1800 segons$

Exemple

Així doncs, quan tenim un minut i mig per exemple, escriurem $1$ minut i la meitat d'aquest que són $30$ segons, és a dir: $1^{'} 30^{″}$ .

Si volem escriure $7$ hores i mitja doncs, escriurem $7$ i la mitja hora en minuts. Atès que una hora són $60$ minuts la meitat d'una hora seran la meitat de $60$ minuts que són $30$ .

Així, set hores i mitja són $7 h 30^{'}$ .

Exemple

També podem fer el procés invers, és a dir, donat un nombre de segons determinar quin número de minuts i / o hores són.

Quants minuts són $1.020$ segons?

$1020 segons = 1020 segons \cdot \frac{1 minut}{60 segons} = \frac{1020}{60} minuts = 17 minuts$

Vegem què fer en el cas que no ens doni un resultat exacte.

Exemple

Suposem que tenim $68$ segons.

A partir d'ara farem servir la notació estàndard de minuts $^{'}$ i segons $^{″}$ per agilitzar l'escriptura i també per acostumar-nos.

Usant factors de conversió ens dóna

$68^{″} = 68^{″} \cdot \frac{1^{'}}{60^{″}} = \frac{68^{'}}{60} = 1, 13333^{'}$

Però expressar $68^{″}$ com un nombre decimal de minuts no és massa útil. El que volem fer és expressar millor per exemple com $68^{″} = 60^{″} + 8^{″} = 1^{'} 8^{″}$ que són un minut i vuit segons.

Per poder expressar així, s'ha de prendre la part sencera del resultat, multiplicar per $60$ i restar a la quantitat original.

Això és:

En el cas anterior el resultat era $1, 13333$ , agafem la part sencera que és $1$ .

La multipliquem per $60$ i ens dóna $60$ .

Ara restem aquest $60$ a la quantitat original que era $68$ .

Ens dóna $8$ .

Per tant tenim $1^{'} 8^{″}$ .

Expressarem el resultat com la part sencera més la resta.

Exemple

Suposem que tenim $24355$ segons. Expressem-ho en hores, minuts i segons:

Primer ho anem a passar a minuts

$24355^{″} = 24355^{″} \cdot \frac{1^{'}}{60^{″}} = \frac{24355^{'}}{60} = {405.9166}^{'}$

Per tant, agafem la part entera d'aquesta divisió: és $405$ i el multipliquem per $60$ : $405 \cdot 60 = 24300$

Ara, a la quantitat original li restem aquest número, obtenint: $24355 - 24300 = 55$

Així doncs, tenim que $24355^{″} = 405^{'} 55^{″}$

Ara hem d'expressar els $405^{'}$ en hores:

Mitjançant el factor de conversió: $405^{'} = 405^{'} \cdot \frac{1 h}{60^{'}} = \frac{405^{'}}{60} = 6, 75 h$

Tornem a fer el procés. Agafem la part entera que és $6$ . La multipliquem per $60$ i obtenim $6 \cdot 60 = 360$ . A la quantitat original li restem aquesta: $405^{'} - 360^{'} = 45$ ' Així doncs, $405^{'} = 6 h 45^{'}$ Per tant $24355^{″} = 6 h 45^{'} 55^{″}$

Un cop sabem expressar les quantitats en hores, minuts i segons, aprendrem a fer operacions entre elles.

Operacions amb temps en hores, minuts i segons

Sumar

Primer és convenient que ordenem, segons amb segons, minuts amb minuts, hores amb hores...

Com sabem cada minut té $60$ segons, llavors en sumar segons tindrem:

$15 segons + 10 segons = 25 segons$ $30 segons + 15 segons = 45 segons$

Però

$30 segons + 45 segons = 75 segons$

En aquest cas, nosaltres sabem que $60 segons = 1 minut$ , si apliquem això al nostre exemple anterior tenim:

$75 segons = 60 segons + 15 segons$

que és igual a $75 segons = 1 minut$ and $15 segons$

Ara si el nombre és molt alt, per exemple 1200 segons, el millor és dividir aquest número per $60$ per obtenir els minuts que representen. És a dir

$\frac{1200}{60} = 20$

és a dir $1200 segons = 20 minuts$ .

De la mateixa forma per a la relació minuts hores. Cada hora consta de $60$ minuts.

Si tens $45 minuts + 25 minuts = 70 minuts$ , és el mateix que

$70 minuts = 60 minuts + 10 minuts = 1 hora i 10 minuts$

En cas de tenir resultats amb decimals, vegem-ne un exemple:

Exemple

$750$ segons, quants minuts són?

Bé prenguem $750$ i dividim-ho per $60$ $\frac{750}{60} = 12, 5$

$750 = 12 minuts + 0, 5 minuts$

Ara, la forma més fàcil de treure els segons que representen aquests $0, 5$ és multiplicant per $60$ ( $0, 5$ està en minuts i per representar de forma correcta necessitem obtenir-ho en segons):

$0, 5 \cdot 60 = 30$ segons. Aquest procediment és el que hem explicat abans.

Finalment tenim que:

$750$ segons $= 12$ minuts i $30$ segons.

Exemple

$\begin{array}{ccccc} α & = & 74 h & 16^{'} & 54^{″} \\ β & = & 28 h & 45^{'} & 13^{″} \end{array}$ $α + β = (74 h 16^{'} 54^{″}) + (28 h 45^{'} 13^{″}) = 102 h 61^{'} 67^{″}$

Així, ens adonem que el que s'ha de fer un cop sumades les quantitats és revisar que si els segons sobrepassen $60$ els hem expressar en minuts i sumar-los als que ja tenim. I el mateix amb els minuts, que si sobrepassen de $60$ també haurem de passar-los a hores.

En el cas anterior tenim $67^{″}$ que són $1^{'} 7^{″}$ . Per tant reescrivim el resultat sumant un minut i deixant $7$ segons. $103 h 62^{'} 7^{″}$

Però com tenim més de $60$ minuts, escrivim una hora més i deixem $2$ minuts (ja que tenim $62^{'}$ ). Per tant: $103 h 2^{'} 7^{″}$ és la suma d'aquestes dues quantitats.

A conseqüència d'això, ja sabem sumar expressions que vinguin en hores, minuts i segons. Només s'han de sumar les quantitats respectivament (hores amb hores, minuts amb minuts i segons amb segons) i després escriure el resultat assegurant-nos que en els segons sempre hi ha un nombre menor que $60$ i en els minuts també hi ha un nombre menor que $60$ .

Restar

Què passarà amb la resta?

Procedirem de la mateixa manera, restarem la xifra de cada unitat amb la de cada unitat. L'únic problema que pot aparèixer és:

Si la quantitat de segons a restar és major que la quantitat original de segons, el que hem de fer és:
- Restar un minut a la quantitat original de minuts.
- Augmentar la quantitat original de segons a $60$ .
Llavors procedirem a restar cadascuna de les quantitats.

Exemple

$4^{'} 11^{″} - 2^{'} 47^{″}$ Atès que $11$ és menor que $47$ , restem un minut a $4$ i afegim $60$ segons a $11$ . La resta quedarà: $3^{'} 71^{″} - 2^{'} 47^{″} = 1^{'} 24^{″}$

Vegem un altre exemple que inclogui hores també:

Exemple

$4 h 23^{'} 11^{″} - 2 h 47^{'} 27^{″}$

En aquest cas $27$ és més gran que $11$ per la qual cosa restem un minut a $23$ que teníem i li sumem $60$ segons a $11$ que teníem: La resta ara és: $4 h 22^{'} 71^{″} - 2 h 47^{'} 27^{″}$

Però ara, ens adonem que en els minuts torna a passar el mateix, que $47$ és major que $22$ minuts de l'original, de manera que li restem $1$ hora a l'original i li sumem $60$ minuts. La resta ara és:

$3 h 82^{'} 71^{″} - 2 h 47^{'} 27^{″} = 1 h 35^{'} 44^{″}$

Multiplicar

Aprenguem a multiplicar nombres expressats en hores minuts i segons per un nombre natural.

El procediment serà multiplicar cada un dels factors (els segons, els minuts i les hores) per aquest nombre natural i després reescriure el resultat de forma correcta, és a dir amb les xifres de segons i minuts menors de $60$ .

Exemple

$\frac{\begin{array}{ccc} 3 h & 12^{'} & 45^{″} \\ \times & 3 \end{array}}{\begin{array}{ccc} 9 h & 36^{'} & 135^{″} \end{array}}$

Per tant passem els $135^{″}$ a minuts: $\frac{135}{60} = 2, 25$ agafem la part entera i multiplicada per $60$ la restem a $135$ , és a dir:

$135 - 2 \cdot 60 = 135 - 120 = 15$

Així, hem de sumar $2$ minuts als $36$ que ja teníem i deixar $15^{″}$ .

Per tant el resultat és $9 h 38^{'} 15^{″}$ .

Dividir

En aquest apartat aprendrem a dividir nombres expressats en hores, minuts i segons per un nombre natural.

Per dividir un temps per un nombre natural:

Es divideixen les hores entre aquest nombre i la resta es multiplica per 60 per passar-lo a minuts. Aquests se sumen als minuts del dividend.
Es divideixen els minuts entre el nombre i la resta es multiplica per $60$ per passar-lo a segons. Aquests se sumen als segons.
Es divideixen els segons entre el nombre.

Exemple

El següent exemple ens permet fer la divisió del temps $34 h 28^{'} 44^{″}$ entre $4$ .

Pas 1 Dividim les hores entre $4$ . $34 = 4 \cdot 8 + 2$

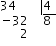
imagen

El residu és $2$ , per tant ho multipliquem per $60$ i el sumem als minuts. $60 \cdot 2 = 120$ Els sumem a $28$ , $120 + 28 = 148^{'}$

Pas 2 Dividim els minuts entre $4$ .

$148 = 4 \cdot 37 + 0$

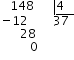
imagen

El residu és $0$ , de manera que no cal sumar-li res als segons.

Pas 3 Dividim els segons entre el número $4$ .

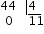
imagen

Finalment escrivim el resultat: $8 h 37^{'} 11^{″}$