Aprendrem a resoldre exercicis que en l'enunciat inclouen qüestions relacionades amb els angles que formen les agulles d'un rellotge.
Vegem algun exemple pràctic directament.
Sent les tres en punt, les agulles del rellotge formen un angle de $$90^\circ$$. Quin angle haurà recorregut l'agulla horària al cap de $$10$$ minuts?
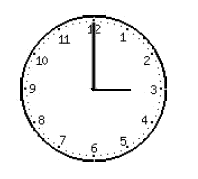
I deu minuts més tard és
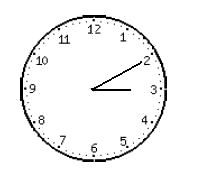
L'angle descrit que recorre el minuter és sempre $$12$$ vegades més gran que l'arc que descriu l'agulla horària. Gràcies a aquesta indicació, podrem conèixer les posicions de les dues com més ens convingui.
Desitgem trobar l'angle que ha recorregut l'agulla horària, que és el mateix que trobar l'arc que ha recorregut. Per tant diguem que $$x$$ és l'arc que descriu l'agulla horària.
El minuter descriu un arc de $$10 + x$$ minuts ja que ens pregunten quin angle formarà quant hagin passat $$10$$ minuts però l'agulla de les hores també va movent-se.
Tenint en compte la relació entre el minuter i l'agulla horària, tenim: $$$10+x=12x$$$
i per tant, $$$x=\frac {10}{11} \ \mbox{minuts}$$$
Així doncs, ja tenim l'arc recorregut per l'agulla horària, és de $$$\frac{10}{11} \ \mbox{minuts}= \frac{10}{11} \ \mbox{minuts} \cdot \frac{60 \ \mbox{segons}}{1 \ \ \mbox{minut}}= \frac{10 \cdot 60}{11} \ \mbox{segons}=$$$ $$$= 54 \ \mbox{segons}$$$
Entenent $$54$$ segons com un submúltiple més petit que el grau.
Vegem un altre tipus de preguntes sobre rellotges.
Un rellotge marca les $$3$$ en punt. Si ens preguntem a quina hora entre les $$3$$ i les $$4$$ es superposaran les agulles, hem de procedir de la següent manera:
Anomenem $$x$$ l'arc que descriu l'agulla horària. De manera que $$15 + x$$ serà l'arc que descriu el minuter, ja que per arribar al principi on hi ha l'hora ha de recórrer els $$15$$ minuts que hi ha des de les $$12$$ (on està inicialment el minuter perquè siguin les $$3$$ en punt) fins a les $$3$$ on està inicialment l'agulla horària. Així, recordant també que l'angle descrit que recorre el minuter és sempre $$12$$ vegades més gran que l'arc que descriu l'agulla horària, es planteja la següent equació: $$$(15+x)=12x$$$
Si aïllem la incògnita $$x$$, és a dir: $$$x= \frac {15}{11} \ \mbox{minuts}$$$
Per tant les agulles es superposaran a les $$3$$ i $$15+x$$ minuts, que exactament són: $$3h \ 16 ' \ 21''$$
Vegem un altre exemple on es treballi la relació de l'angle que hi ha entre el minuter i l'agulla horària.
Considerem que un rellotge marca les $$2$$ en punt. A quina hora formaran les seves agulles per primera vegada un angle recte?
Les agulles del rellotge formen un angle recte quan marca aproximadament les $$2h \ 25'$$. Això ho deduïm del fet que quan l'hora marca les $$2$$ en punt, perquè el minuter estigui en angle recte ha d'estar $$15$$ minuts més que el que marca l'hora, per tant, $$15$$ minuts més que el nombre $$2$$ (corresponent a $$10$$ minuts) serà $$25$$.
Així doncs, si $$x$$ és l'arc que descriu l'agulla horària, i $$25 + x$$ el que descriu el minuter, gràcies a la relació que l'angle descrit que recorre el minuter és sempre $$12$$ vegades més gran que l'arc que descriu l'agulla horària, tenim que: $$$25+x=12x$$$
En aquest cas, el resultat que s'obté és: $$$ x=\frac{25}{11} \ \mbox{minuts}$$$
Per tant les agulles del rellotge conformaran un angle de $$90^\circ$$ a les $$2h$$: $$$ 25+x \ \mbox{minuts}$$$ En aquest cas això és: $$$2h \ 27 ' \ 16''$$$