Un angle és la porció del pla determinada per dues semirectes amb origen comú. Les semirectes que el formen s'anomenen costats de l'angle i el punt comú, vèrtex.
El que caracteritza a un angle és l'obertura dels seus costats. Per tant a partir d'ara ens referirem a angle quan vulguem parlar de l'obertura entre dues línies de qualsevol tipus que concorren en un punt comú anomenat vèrtex.
Vegem un dibuix d'un angle:
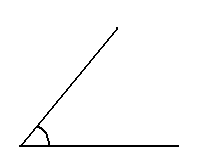
L'obertura entre les dues semirectes és l'angle.
Si els costats d'un angle $$a$$ estan més oberts que els d'un altre angle $$b$$ es diu que $$a$$ és major que $$b$$.
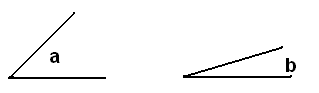
Donats aquests dos angles, com l'obertura del primer és més gran que la del segon, l'angle $$a$$ és més gran que l'angle $$b$$.
Notació: Per nomenar els angles, diferenciarem dos tipus d'ells.
Quan l'angle està format per vèrtexs d'un polígon utilitzarem els símbols $$\widehat{abc}$$, que significa que és l'angle que formen els dos segments que es formen en ajuntar els vèrtexs $$ab$$ amb el $$bc$$.
Podem també anomenar mitjançant una lletra grega o amb un nombre que es col·loca dins de l'angle que no formen part de cap polígon.
.gif)
En aquest cas, l'angle blau en diem $$\widehat{ABC}$$ ja que és el format pels segments $$AB$$ i $$BC$$.
L'angle verd serà $$\widehat{BCA}$$, i el vermell serà $$\widehat{CAB}$$.
Per a qualsevol altre angle que no formi part d'un polígon amb vèrtexs etiquetats també podem emprar lletres gregues per anomenar-los.
Recordem que:
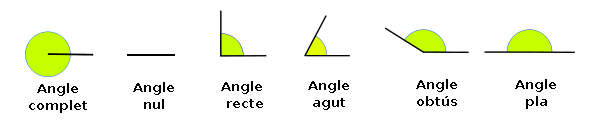
- Un angle nul, és l'angle definit per dues rectes que coincideixen. Per tant no hi ha amplitud de rotació.
- Un angle recte, és l'angle definit per dues rectes perpendiculars.
- Un angle pla, és l'angle definit per dues rectes que tenen la mateixa direcció però sentits oposats. Per tant recórre un semiplà, és a dir, la meitat del pla.
- Un angle complet, és l'angle que abarca tot el pla. Per tant recórre el pla complet.
- Els angles menors que un angle recte s'anomenen angles aguts.
- Els angles majors que un angle recte s'anomenen angles obtusos.
Representació gràfica d'angles notables