Problemas de relojes

Ejemplo

Siendo las tres en punto, las agujas del reloj forman un ángulo de ${90}^{\circ }$. ¿Qué ángulo habrá recorrido la aguja horaria al cabo de $10$ minutos?

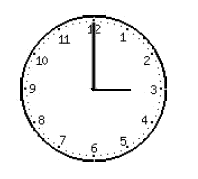
Y diez minutos más tarde es

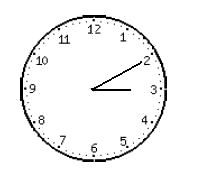
El ángulo descrito que recorre el minutero es siempre 12 veces mayor que el arco que describe la aguja horaria.

Gracias a esta indicación, podremos conocer las posiciones de una y otra como más nos convenga.

Deseamos encontrar el ángulo que ha recorrido la aguja horaria, que es lo mismo que encontrar el arco que ha recorrido.

Por lo tanto digamos que $x$ es el arco que describe la aguja horaria.

El minutero describe un arco de $10+x$ minutos puesto que nos preguntan qué ángulo formará en cuanto hayan pasado $10$ minutos pero la aguja de las horas también va moviéndose.

Teniendo en cuenta la relación entre el minutero y la aguja horaria, tenemos: $$10+x=12x$$

por lo que, $$x=\frac{10}{11}\text{minutos}$$

Así pues, ya tenemos el arco recorrido por la aguja horaria, es de $$\frac{10}{11}\text{minutos}=\frac{10}{11}\text{minutos}\cdot \frac{60\text{segundos}}{1\text{minuto}}=\frac{10\cdot 60}{11}\text{segundos}=$$ $$=54\text{segundos}$$

Entendiendo $54$ segundos como un submúltiplo más pequeño que el grado.

Ejemplo

Un reloj marca las $3$ en punto. Si nos preguntamos a qué hora entre las $3$ y las $4$ se superpondrán las agujas, debemos proceder de la siguiente manera:

Llamamos $x$ al arco que describe la aguja horaria. De manera que $15+x$ será el arco que describe el minutero, puesto que para llegar al principio donde está la hora debe recorrer los $15$ minutos que hay desde las $12$ (donde está inicialmente el minutero para que sean las $3$ en punto) hasta las $3$ donde está inicialmente la aguja horaria.

Así, recordando también que el ángulo descrito que recorre el minutero es siempre 12 veces mayor que el arco que describe la aguja horaria, se plantea la siguiente ecuación: $$(15+x)=12x$$

Si aislamos la incógnita $x$, esto es: $$x=\frac{15}{11}\text{minutos}$$

Por lo tanto las agujas se superpondrán a las $3$ y $15+x$ minutos, que exactamente son: $3h{16}^{\prime }{21}^{″}$

Ejemplo

Consideramos que un reloj marca las $2$ en punto. ¿A qué hora formarán sus agujas por primera vez un ángulo recto?

Las agujas del reloj forman un ángulo recto cuando marca aproximadamente las $2h{25}^{\prime }$. Esto lo deducimos del hecho en que cuando la hora marca las $2$ en punto, para que el minutero esté en ángulo recto debe estar $15$ minutos más que lo que marca la hora, por lo tanto, $15$ minutos más que el número $2$ (correspondiente a $10$ minutos) será $25$.

Así pues, si $x$ es el arco que describe la aguja horaria, y $25+x$ el que describe el minutero, gracias a la relación que el ángulo descrito que recorre el minutero es siempre 12 veces mayor que el arco que describe la aguja horaria, tenemos que: $$25+x=12x$$

En este caso, el resultado que se obtiene es: $$x=\frac{25}{11}\text{minutos}$$

Por lo tanto las agujas del reloj conformarán un ángulo de ${90}^{\circ }$ a las $2h$: $$25+x\text{minutos}$$ En este caso esto es: $$2h{27}^{\prime }{16}^{″}$$