We are going to try to solve the following example with the basic tools of Probabilities.
A screw factory has two machines, the M1, which is old, and does 75 % of all the screws, and the M2, newer but small, that does 25 % of the screws. The M1 does 4 % of defective screws, while the M2 just does 2 % of defective screws. If we choose a screw at random: what is the probability that ir turns out to be defective?
We consider the following events:
$$M1$$ = "being produced by the machine 1"
(and therefore, $$\overline{M1}=M2$$ ="being produced by the machine 2")
$$D$$ = "defective screw"
If we represent our problem in a tree, we can compute the probability more easily.
In the diagram we can see the branches that we are interested in (in dark orange).
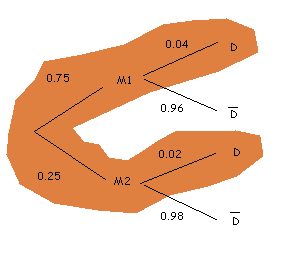
The top branch, "being produced by machine 1 and being defective", has probability $$0,75 \cdot 0,04 = 0,03$$, that is, $$3$$%. The bottom branch, "being produced by machine 2 and being defective", has probability $$0,2\cdot 0,02 = 0,005$$, that is to say $$0,5$$%.
Therefore, the probability of being defective is:
$$$P(D) = 0,75\cdot 0,04 + 0,250\cdot 0,02 = 0.035$$$
Let's analyse what we have done. The probabilities with which we have worked are in a way conditional probabilities: $$P(D/M1)$$ is the probability that it turns out to be defective given that it has been produced with machine 1.
So, we can re-write our result as:
$$$ P(D) = P(M1)\cdot P(D/M1) + P(M2)\cdot P(D/M2)$$$
We can generalize this result with the theorem or law of total probability.
Law of total probability:
Let $$A_1,A_2,\ldots, A_n$$ be a complete system of events and $$B$$ any event associated with the same experiment. Then, we have :
$$$ P(B)=P(A_1)\cdot P(B/A_1)+P(A_2)\cdot P(B/A_2)+\ldots+ P(A_n)\cdot P(B/A_n) $$$
Let's recall that a complete system of events or partition is a set of incompatible events two by two (that is, that they cannot happen simultaneously), and such that the union of all of them is the complete sample space. A particular example of a partition of the sample space is each of their events. Unless we say so, we will always assume that the events in a partition always have a non zero probability. Otherwise we could always eliminate such an evenet and we would obtain a smaller partition of the sample space.
Let's see other examples where we can apply this result.
We have three boxes with light bulbs. The first one contains $$10$$ bulbs, with $$4$$ of them broken; in the second one there are $$6$$ light bulbs, and only one broken, and in the third one there are three broken light bulbs out of eight. What is the probability that if we choose a box at random and we take a light bulb, this is broken?
We will write $$C1$$, $$C2$$, $$C3$$ if we choose the boxes 1, 2, and 3, respectively.
Since the election is random, we have probability $$\dfrac{1}{3}$$ of choosing each box.
The event that we are interested in is $$F =$$ "broken light bulb", or if we write $$\overline{F} =$$ "working bulb".
We represent it in a tree:
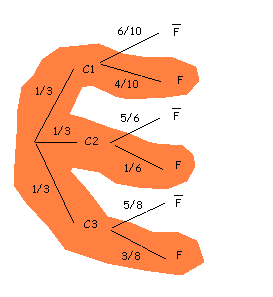
In dark orange we observe the branches of the tree that lead to the event that we are interested in, i.e. "broken light bulbs".
$$(C1, C2, C3)$$ is a partition of the sample space, since we will always choose one of three boxes (in other words, its union is the whole), and we cannot choose more than one box (i.e., they are two by two incompatible).
We apply, then, the law of total probability:
$$$ \begin{array}{rl} P(F) =& P(C1)\cdot P(F/C1) + P(C2)\cdot P(F/C2) + P(C3)\cdot P(F/C3) \\ =& \dfrac{1}{3}\cdot\dfrac{4}{10}+\dfrac{1}{3}\cdot\dfrac{1}{6}+ \dfrac{1}{3}\cdot\dfrac{3}{8} = \dfrac{4}{30}+\dfrac{1}{18}+\dfrac{3}{24}= \dfrac{113}{360} \end{array}$$$
As we can see, to apply the theorem of the total probability is the same as to compute the probability using the tree.
The only thing we have to care about is to compute the probabilities for each of the branches.
A bag contains three red balls and two blue balls. We do two experiments:
i) We remove successively, and with replacement, two balls and observe their colour. What is the probability of $$S =$$ "to extract a red ball and a blue one, without taking into account the order"?
ii) We remove successively, but without replacement, two balls and observe their colour. What is the $$P(S)$$ in this case?
This is a very frequent experiment: when we remove something with replacement, it means that when we remove the ball from the bag, we then introduce it back. If it is without replacement, we keep the ball out. This will influence the probability of the second ball being one color or another.
Let's consider the events: $$R =$$ "to remove a red ball", $$A =\overline{R} =$$ "to remove a blue ball.
Our sample space is: $$\Omega=\{RR,RA,AR,AA\}$$, and the events that we are interested in are $$RA$$ and $$AR$$.
i) We represent our problem in a tree.
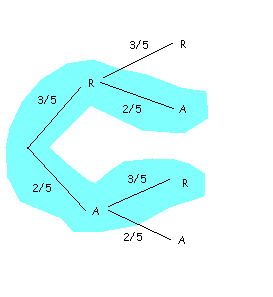
Using the law of total probability, $$$ P (S) = P (R)\cdot P (A / R) + P (A)\cdot P (R / A) = \dfrac{3}{5}\cdot\dfrac{2}{5}+\dfrac{2}{5}\cdot\dfrac{3}{5}= \dfrac{12}{25}$$$
ii) In this case, the second time that we remove a ball, the probabilities will be different, depending on whether the first ball was red or blue.
For example, $$P (A / R) =$$ "probability of removing a blue ball the second time, knowing that in the first one we have removed a red one" $$= \dfrac{2}{4}$$, since upon removing a red ball from the bag, there will be two blue balls remaining.
In this case, our tree is the following (compute the conditional probabilities, and verify that you obtain the same result):
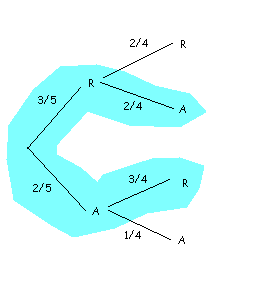
And so, by virtue of the law of total probability, we have a different result from that of the previous case: $$$P (S) = P (R)\cdot P (A / R) + P (A)\cdot P (R / A) = \dfrac{3}{5}\cdot\dfrac{2}{4}+\dfrac{2}{5}\cdot\dfrac{3}{4}= \dfrac{12}{20}$$$
We will finish this level with a more complicated problem that will be useful to see that the way of solving more complicated problems is the same that what we have done until now.
Suppose we have $$250$$ doctors from Europe meeting in a conference. Among these $$115$$ are Germans; $$65$$, French, and $$70$$ Englishmen. We also know that, 75 % of the Germans, 60 % of the French and 65 % of the Englishmen are in favour of using a new vaccine for the flu. In order to decide whether the vaccine is finally used they agree on the following: among all the doctors they select at random three doctors, who answer if they are in favour or not (with replacement). Remember that with replacement means that the same doctor can be selected all three times (or two times for the matter). The vaccine is approved out of these three picks, at least two agree on using the vaccine. What is the probability that this occurs?
Let's consider the following events: $$A =$$ "German doctor", $$F =$$ "French doctor", $$I =$$ "English doctor", as well as $$V =$$ "to be in favour of the vaccine" (and therefore, $$\overline{V} =$$ "to be against of the vaccine").
It is a question of a compounded election: we choose three doctors, each of which can be in favor or against using the vaccine.Our sample space would be: $$$\Omega=\{ (V,V,V),(V,V,\overline{V}),(V,\overline{V},V),(V,\overline{V},\overline{V}), \\ (\overline{V},V,V),(\overline{V},V,\overline{V}),(\overline{V},\overline{V},V),(\overline{V},\overline{V},\overline{V}) \}$$$
The are four favorable cases: $$(V,V,V)$$, $$(V,V,\overline{V})$$, $$(V,\overline{V},V)$$, $$(\overline{V},V,V)$$.
Now , in order to choose every doctor, we do another compounded experiment: we choose randomly a country between $$A$$, $$F$$, $$I$$, and when the doctor is chosen then he must say whether he is in favor ($$V$$), or against ($$\overline{V}$$) the vaccine.
We represent our problem in a tree. We have to be sure that we repeat this experiment three times, one for every vote. Note again that it is a case with replacement, since the same doctor can be picked more than once. Thus we have three votes coming out from the same tree, represented below:
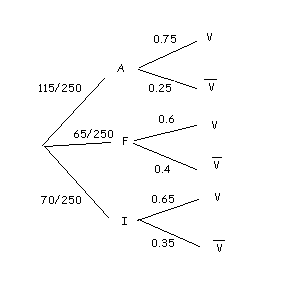
Our sample space for every experiment is $$\Omega_i=\{ (A,V), (A,\overline{V}), (F,V), (F,\overline{V}), (I,V), (I,\overline{V}) \}$$.
What is the probability that a doctor chosen at random is in favor of the vaccine?
Using the law of total probability,
$$$ P (V) = P (A)\cdot P (V / A) + P (F)\cdot P (V / F) + P (I)\cdot P (I / F)$$$
Seen through other lenses, we add the probability of all the branches that finish in $$V$$.
Substituting, $$$P(V)=\dfrac{115}{250}\cdot 0,75 +\dfrac{65}{250}\cdot 0,6+ \dfrac{70}{250}\cdot 0,65= 0,345+ 0,156+ 0,182 = 0,683 $$$
That is, a probability of 68,3%. Since we know that $$P(\overline{V})=1-P(V)$$, we also have that $$P(\overline{V})=1-0,683=0,317$$, or in words, a probability of 31,7%.
We repeat this experiment three times. We have four favorable cases:
- Case $$(V,V,V)$$: its probability is $$0,683\cdot0,683\cdot0,683 = 0,319$$.
- Case $$(V,V,\overline{V})$$: its probability is $$0,683\cdot 0,683\cdot 0,317 = 0,148$$.
- Case $$(V,\overline{V},V)$$: its probability is $$0,683\cdot 0,317\cdot 0,683 = 0,148$$.
- Case $$(\overline{V},V,V)$$: its probability is $$0,317\cdot 0,683\cdot 0,683 = 0,148$$.
Finally, the probability of approving the vaccine is: $$$0,319 + 0,148 + 0,148 + 0,148 = 0,763$$$ that is to say, of 76,3%.
Observació 1:
Since we are not concerned with the order with which the doctors are chosen, but rather with whether they are in favor of the vaccine or not, we might think that our sample space is $$\Omega=\{\{V,V,V\}, \{V,V,\overline{V}\}, \{V,\overline{V},V\}, \{\overline{V},V,V\}\}$$.
Note that, instead of writing the elementary events with brackets, "( )", ewe write them with "{ }", to signify that our results are wihtout order. We will analyze this with some more depth in the combinatorial analysis cell.
There are two favorable cases: $$\{V,V,V\}$$ and $$ \{V,V,\overline{V}\}$$, although we have to be sure that the second one counts three times, since it corresponds in fact to three unordered events. Thus we would calculate, in the same way, the probability of every case, and would obtain the total probability making $$P(\text{"as minimum two affirmative votes"}) = P(\{V,V,V\})+ 3P(\{V,V,\overline{V}\})$$, The result should not change if we follow this strategy.
Observation 2:
It may look a bit weird that a single doctor can be chosen three times. In fact, if we do not allow the same doctor to vote more than once the result does not change much. This is because of the large number of doctors taking part in the conference. You are entitled, however, to redo the problem assuming that each doctor can vote only once, that is, that there is no replacement.