Teorema de la probabilidad total

Una fábrica de tornillos tiene dos máquinas, la M1, que es más antigua, y hace el $$75$$% de todos los tornillos, y la M2, más nueva pero pequeña, que hace el $$25$$% de los tornillos. La M1 hace un $$4$$% de tornillos defectuosos, mientras que la M2 tan sólo hace un $$2$$% de tornillos defectuosos. Si escogemos un tornillo al azar, ¿qué probabilidad hay de que salga defectuoso?

Consideramos los siguientes sucesos:

$$M1$$ = "ser producido por la máquina 1"

(y entonces $$\overline{M1}=M2$$ ="ser producido por la máquina 2")

$$D$$ = "tornillo defectuoso"

Si representamos nuestro problema en un diagrama de árbol, podemos calcular la probabilidad más fácilmente.

En el diagrama están marcadas las dos ramas que nos interesan.

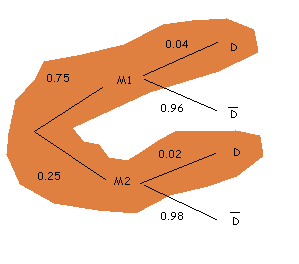
La rama superior, "ser producido por la máquina 1 y ser defectuoso", tiene probabilidad $$0,75 \cdot 0,04 = 0,03$$, és a dir, un $$3$$%. La rama inferior, "ser producido por la máquina 2 y ser defectuoso", tiene probabilidad $$0,2\cdot 0,02 = 0,005$$, és a dir, un $$0,5$$%.

Por lo tanto, la probabilidad de ser defectuoso es:

$$$P(D) = 0,75\cdot 0,04 + 0,250\cdot 0,02 = 0.035$$$

Observemos lo que hemos hecho. Las probabilidades con las que hemos trabajado son de hecho probabilidades condicionadas: $$P(D/M1)$$ es, precisamente, la probabilidad de que salga defectuoso si sabemos que lo ha producido la máquina 1.

Así pues, podemos reescribir nuestro resultado como:

$$$ P(D) = P(M1)\cdot P(D/M1) + P(M2)\cdot P(D/M2)$$$

Tenemos tres cajas con bombillas. La primera contiene $$10$$ bombillas, de las cuales hay cuatro fundidas; en la segunda hay seis bombillas, y tan sólo una fundida, y en la tercera hay tres bombillas fundidas de un total de ocho. ¿Cuál es la probabilidad de que si escogemos una caja al azar, y cogemos una bombilla, ésta esté fundida?

Escribiremos $$C1$$, $$C2$$, $$C3$$ si escogemos las cajas 1, 2, y 3, respectivamente.

Como la elección es al azar, tenemos probabilidad $$\dfrac{1}{3}$$ de escoger cada caja.

El suceso que nos interesa es $$F =$$ "bombilla fundida", por lo que $$\overline{F} =$$ "bombilla no fundida".

Lo representamos en un diagrama en árbol:

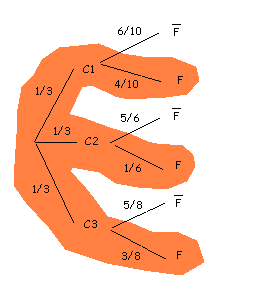
Están marcadas en naranja las tres ramas que nos interesan, las que acaban en "bombilla fundida".

$$(C1, C2, C3)$$ es un sistema completo de sucesos, ya que siempre escogeremos una de las tres cajas (es decir, su unión es el total), y no podemos escoger más de una (es decir, son incompatibles dos a dos).

Aplicamos, pues, el teorema de la probabilidad total:

$$$ \begin{array}{rl} P(F) =& P(C1)\cdot P(F/C1) + P(C2)\cdot P(F/C2) + P(C3)\cdot P(F/C3) \\ =& \dfrac{1}{3}\cdot\dfrac{4}{10}+\dfrac{1}{3}\cdot\dfrac{1}{6}+ \dfrac{1}{3}\cdot\dfrac{3}{8} = \dfrac{4}{30}+\dfrac{1}{18}+\dfrac{3}{24}= \dfrac{113}{360} \end{array}$$$

Una bolsa contiene tres bolas rojas y dos bolas azules. Hacemos dos experimentos:

i) Extraemos sucesivamente, y con reposición, dos bolas y observamos su color. ¿Cuál es la probabilidad de $$S=$$ "extraer una bola roja y una azul, sin que importe el orden"?

ii) Extraemos sucesivamente, pero sin reposición, dos bolas y observamos su color. ¿Cuál es la $$P(S)$$ en este caso?

Este es un experimento muy frecuente: cuando extraemos algo con reposición, quiere decir que cuando sacamos la bola, la volvemos a introducir en la bolsa. Si es sin reposición, nos quedamos la bola que hemos sacado, por lo que esto influirá en la probabilidad de que la segunda sea de un color o de otro.

Consideremos los sucesos: $$R =$$ "sacar una bola roja", $$A =\overline{R} =$$ "sacar una bola azul".

Nuestro espacio muestral es: $$\Omega=\{RR,RA,AR,AA\}$$, y los sucesos que nos interesan son $$RA$$ y $$AR$$.

i) Representamos nuestro problema en un diagrama en árbol.

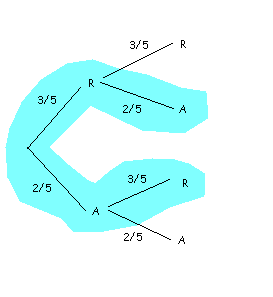
Por el teorema de la probabilidad total, $$$ P (S) = P (R)\cdot P (A / R) + P (A)\cdot P (R / A) = \dfrac{3}{5}\cdot\dfrac{2}{5}+\dfrac{2}{5}\cdot\dfrac{3}{5}= \dfrac{12}{25}$$$

ii) En este caso, la segunda vez que sacamos una bola, las probabilidades serán diferentes, según si hemos cogido una bola roja o una azul la primera vez.

Por ejemplo, $$P (A / R) =$$ "probabilidad de sacar una bola azul la segunda vez, sabiendo que en la primera hemos sacado una roja" $$= \dfrac{2}{4}$$, ya que como hemos sacado una bola roja de la bolsa, quedan dos bolas azules de un total de cuatro bolas.

En este caso, nuestro diagrama en árbol es el siguiente (calcula las probabilidades condicionadas, y comprueba que te da lo mismo):

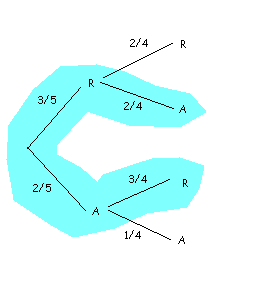
Así pues, por el teorema de la probabilidad total, tenemos un resultado diferente al del apartado anterior: $$$P (S) = P (R)\cdot P (A / R) + P (A)\cdot P (R / A) = \dfrac{3}{5}\cdot\dfrac{2}{4}+\dfrac{2}{5}\cdot\dfrac{3}{4}= \dfrac{12}{20}$$$

En un congreso se reúnen $$250$$ médicos de Europa, de los cuales $$115$$ son alemanes; $$65$$, franceses, y $$70$$ ingleses. De estos médicos, el $$75$$% de los alemanes, el $$60$$% de los franceses y el $$65$$% de los ingleses están a favor de utilizar una nueva vacuna para la gripe. Para escoger finalmente si se aplica la vacuna, se hace lo siguiente: de entre la lista de médicos, se selecciona al azar tres veces un médico, que responde si está a favor o no. Puede darse el caso de que se seleccione más de una vez al mismo médico, es decir, al votar, no se le tacha de la lista. Como se decide por mayoría, ¿cuál es la probabilidad de que como mínimo dos votos sean a favor de utilizar la vacuna?

Consideremos los siguientes sucesos: $$A =$$ "médico alemán", $$F =$$ "médico francés", $$I =$$ "médico inglés", así como $$V =$$ "estar a favor de la vacuna" (y por lo tanto, $$\overline{V} =$$ "estar en contra de la vacuna").

Se trata de una elección compuesta: escogemos tres médicos, cada uno de los cuales puede estar a favor o en contra de utilizar la vacuna. Nuestro espacio muestral total sería:
$$$\Omega=\{ (V,V,V),(V,V,\overline{V}),(V,\overline{V},V),(V,\overline{V},\overline{V}), \\ (\overline{V},V,V),(\overline{V},V,\overline{V}),(\overline{V},\overline{V},V),(\overline{V},\overline{V},\overline{V}) \}$$$

Los casos favorables son cuatro: $$(V,V,V)$$, $$(V,V,\overline{V})$$, $$(V,\overline{V},V)$$, $$(\overline{V},V,V)$$.

Ahora bien, para escoger cada médico en realidad hacemos otro experimento compuesto: escogemos aleatoriamente un país entre $$A$$, $$F$$, $$I$$, y una vez escogido el médico, éste puede estar a favor ($$V$$), o en contra ($$\overline{V}$$) de aplicar la vacuna.

Representamos nuestro problema en un diagrama en árbol. Tenemos que tener claro que este experimento lo repetimos tres veces, una para cada voto. Se trata de una votación "con reposición", puesto que el mismo médico puede votar más de una vez. De este modo, la situación es la misma para las tres votaciones.

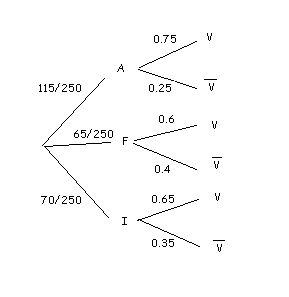
Nuestro espacio muestral de cada experimento es $$\Omega_i=\{ (A,V), (A,\overline{V}), (F,V), (F,\overline{V}), (I,V), (I,\overline{V}) \}$$. ¿Cuál es la probabilidad de que un médico escogido al azar esté a favor de la vacuna?

Por el teorema de la probabilidad total,

$$$ P (V) = P (A)\cdot P (V / A) + P (F)\cdot P (V / F) + P (I)\cdot P (I / F)$$$

Visto de otro modo, sumamos la probabilidad de todas las ramas que acaban en $$V$$.

Sustituyendo, $$$P(V)=\dfrac{115}{250}\cdot 0,75 +\dfrac{65}{250}\cdot 0,6+ \dfrac{70}{250}\cdot 0,65= 0,345+ 0,156+ 0,182 = 0,683 $$$

Es decir, una probabilidad del 68,3%. Como sabemos que $$P(\overline{V})=1-P(V)$$, también tenemos que $$P(\overline{V})=1-0,683=0,317$$, o lo que es lo mismo, una probabilidad del 31,7%.

Repetimos esta elección tres veces. Tenemos cuatro casos favorables:

• Caso $$(V,V,V)$$: su probabilidad es $$0,683\cdot0,683\cdot0,683 = 0,319$$.
• Caso $$(V,V,\overline{V})$$: su probabilidad es $$0,683\cdot 0,683\cdot 0,317 = 0,148$$.
• Caso $$(V,\overline{V},V)$$: su probabilidad es $$0,683\cdot 0,317\cdot 0,683 = 0,148$$.
• Caso $$(\overline{V},V,V)$$: su probabilidad es $$0,317\cdot 0,683\cdot 0,683 = 0,148$$.

Finalmente, la probabilidad de tener como mínimo dos votos a favor es: $$$0,319 + 0,148 + 0,148 + 0,148 = 0,763$$$ es decir, del 76,3%.

Observación 1:

En este caso no nos importa el orden en que escogemos los médicos, tan sólo si están a favor o no de la vacuna: por esto, podríamos considerar que nuestro espacio muestral es $$\Omega=\{\{V,V,V\}, \{V,V,\overline{V}\}, \{V,\overline{V},V\}, \{\overline{V},V,V\}\}$$, sin tener en cuenta el orden en que han salido escogidos los médicos, sino tan sólo si están a favor o en contra.

En vez de escribir los sucesos elementales con paréntesis "( )", los escribimos en este caso con llaves "{ }", es la forma de decir que nuestros resultados están desordenados. Trataremos esto con más profundidad en el tema de combinatoria.

Los casos favorables son dos, en este caso: $$\{V,V,V\}$$ y $$ \{V,V,\overline{V}\}$$, aunque tenemos que tener claro que el segundo cuenta por tres, ya que se corresponde en realidad con tres sucesos ordenados. De esta forma, calcularíamos del mismo modo la probabilidad de cada caso, y obtendríamos la probabilidad total haciendo $$P(\text{"como mínimo dos votos a favor"}) = P(\{V,V,V\})+ 3P(\{V,V,\overline{V}\})$$, por lo que la probabilidad acaba saliendo la misma tanto si los consideramos ordenados como desordenados.

Observación 2:

Puede parecer extraño que en nuestro problema dejemos que un médico pueda votar más de una vez, sería más realista que un médico sólo pudiera votar como máximo una vez. Lo que sucede en realidad es que la probabilidad de que esto pase es tan pequeña, que normalmente estudiaríamos el problema de esta manera, ya que probablemente hacemos un error mayor redondeando los decimales de los resultados parciales que complicando el problema para que un médico sólo pueda votar una vez. No obstante, es interesante intentar resolverlo suponiendo que un médico sólo puede votar una vez (entonces tendríamos que calcular una probabilidad condicionada diferente para cada elección del médico), y compararlo con el resultado que hemos encontrado.