Teorema de la probabilitat total

Exemple

Una fàbrica de cargols té dues màquines, la M1, que és més antiga, i fa el $75$% de tots els cargols, i la M2, més nova però petita, que fa el $25$% dels cargols. La M1 fa un $4$% de cargols defectuosos, mentre que la M2 tan sols fa un $2$% de cargols defectuosos. Si escollim un cargol a l'atzar, quina probabilitat hi ha que surti defectuós?

Considerem els següents esdeveniments:

$M1$ = "ser produït per la màquina 1"

(i llavors $\overline{M1}=M2$ ="ser produït per la màquina 2")

$D$ = "cargol defectuós"

Si representem el nostre problema en un diagrama d'arbre, podem calcular la probabilitat més fàcilment.

En el diagrama estan marcades les dues branques que ens interessen.

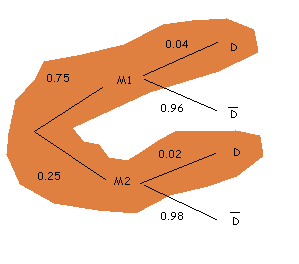
La branca superior, "ser produït per la màquina 1 i ser defectuós", té probabilitat $0,75\cdot 0,04=0,03$, és a dir, un $3$%. La branca inferior, "ser produït per la màquina 2 i ser defectuós", té probabilitat $0,2\cdot 0,02=0,005$, és a dir, un $0,5$%.

Per tant, la probabilitat de ser defectuós és:

$$P(D)=0,75\cdot 0,04+0,250\cdot 0,02=0.035$$

Observem el que hem fet. Les probabilitats amb les quals hem treballat són de fet probabilitats condicionades: $P(D/M1)$ és, precisament, la probabilitat que surti defectuós si sabem que l'ha produït la màquina 1.

Així doncs, podem reescriure el nostre resultat com:

$$P(D)=P(M1)\cdot P(D/M1)+P(M2)\cdot P(D/M2)$$

Exemple

Tenim tres caixes amb bombetes. La primera conté $10$ bombetes, de les quals hi ha quatre foses, en la segona hi ha sis bombetes, i tan sols una fosa, i en la tercera hi ha tres bombetes foses d'un total de vuit. Quina és la probabilitat que si escollim una caixa a l'atzar, i agafem una bombeta, aquesta estigui fosa?

Escriurem $C1$, $C2$, $C3$ si triem les caixes 1, 2, i 3, respectivament.

Com que la elecció és l'atzar, tenim probabilitat ${\displaystyle \frac{1}{3}}$ de triar cada caixa.

El succés que ens interessa és $F=$ "bombeta fosa", de manera que $\bar{F}=$ "bombeta no fosa".

El representem en un diagrama en arbre:

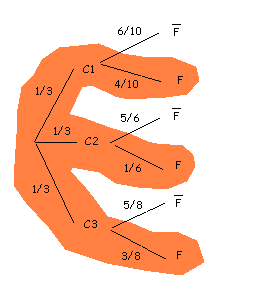
Estan marcades en taronja les tres branques que ens interessen, les que acaben en "bombeta fosa".

$(C1,C2,C3)$ és un sistema complet de successos, ja que sempre escollirem una de les tres caixes (és a dir, la seva unió és el total), i no en podem escollir més d'una (és a dir, són incompatibles 2-2).

Apliquem, doncs, el teorema de la probabilitat total:

$$\begin{array}{rl}P(F)=& P(C1)\cdot P(F/C1)+P(C2)\cdot P(F/C2)+P(C3)\cdot P(F/C3)\\ =& {\displaystyle \frac{1}{3}}\cdot {\displaystyle \frac{4}{10}}+{\displaystyle \frac{1}{3}}\cdot {\displaystyle \frac{1}{6}}+{\displaystyle \frac{1}{3}}\cdot {\displaystyle \frac{3}{8}}={\displaystyle \frac{4}{30}}+{\displaystyle \frac{1}{18}}+{\displaystyle \frac{3}{24}}={\displaystyle \frac{113}{360}}\end{array}$$

Exemple

Una bossa conté tres boles vermelles i dues boles blaves. Fem dos experiments:

i) extraiem successivament, i amb reposició, dues boles i observem el seu color. Quina és la probabilitat de $S=$ "extreure una bola vermella i una blava, sense que importi l'ordre"?

ii) extraiem successivament, però sense reposició, dues boles i observem el seu color. Quina és la $P(S)$ en aquest cas?

Aquest és un experiment molt freqüent: quan extraiem alguna cosa amb reposició, vol dir que quan traiem la bola, la tornem a introduir en la borsa. Si és sense reposició, ens vam quedar la bola que hem tret, per tant tan influirà en la probabilitat que la segona sigui d'un color o d'un altre.

Considerem els successos: $R=$ "treure una bola vermella", $A=\bar{R}=$ "treure una bola blava".

El nostre espai mostral és: $\mathrm{\Omega }=\{RR,RA,AR,AA\}$, i els esdeveniments que ens interessen són $RA$ i $AR$.

i) Representem el nostre problema en un diagrama en arbre.

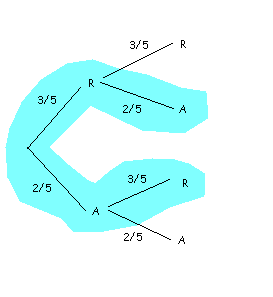
Pel teorema de la probabilitat total, $$P(S)=P(R)\cdot P(A/R)+P(A)\cdot P(R/A)={\displaystyle \frac{3}{5}}\cdot {\displaystyle \frac{2}{5}}+{\displaystyle \frac{2}{5}}\cdot {\displaystyle \frac{3}{5}}={\displaystyle \frac{12}{25}}$$

ii) En aquest cas, la segona vegada que traiem una bola, les probabilitats seran diferents, segons si hem agafat una bola vermella o una blava la primera vegada.

Per exemple, $P(A/R)=$ "probabilitat de treure una bola blava la segona vegada, sabent que a la primera hem tret una vermella" $={\displaystyle \frac{2}{4}}$, ja que com hem tret una bola vermella de la bossa, queden dues boles blaves d'un total de quatre boles.

En aquest cas, el nostre diagrama en arbre és el següent (calcula les probabilitats condicionades, i comprova que et dóna el mateix):

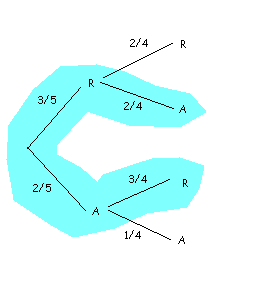
Així doncs, pel teorema de la probabilitat total, tenim un resultat diferent al de l'apartat anterior: $$P(S)=P(R)\cdot P(A/R)+P(A)\cdot P(R/A)={\displaystyle \frac{3}{5}}\cdot {\displaystyle \frac{2}{4}}+{\displaystyle \frac{2}{5}}\cdot {\displaystyle \frac{3}{4}}={\displaystyle \frac{12}{20}}$$

Exemple

En un congrés es reuneixen $250$ metges d'Europa, dels quals $115$ són alemanys, $65$, francesos, i $70$ anglesos. D'aquests metges, el 75% dels alemanys, el 60% dels francesos i el 65% dels anglesos estan a favor d'utilitzar una nova vacuna per la grip. Per escollir finalment si s'aplica la vacuna, es fa el següent: entre la llista de metges, es selecciona a l'atzar tres vegades un metge, que respon si està a favor o no. Es pot donar el cas que se seleccioni més d'una vegada al mateix metge, és a dir, al votar, no se l'esborra de la llista. Com es decideix per majoria, quina és la probabilitat que com a mínim dos vots siguin a favor d'utilitzar la vacuna?

Considerem els següents esdeveniments: $A=$ "metge alemany", $F=$ "metge francès", $I=$ "metge anglès", així com $V=$ "estar a favor de la vacuna" (i per tant, $\bar{V}=$ "estar en contra de la vacuna").

Es tracta d'una elecció composta: escollim tres metges, cadascun dels quals pot estar a favor o en contra d'utilitzar la vacuna. El nostre espai mostral total seria: $$\begin{gathered} \mathrm{\Omega }=\{(V,V,V),(V,V,\bar{V}),(V,\bar{V},V),(V,\bar{V},\bar{V}), \\ (\bar{V},V,V),(\bar{V},V,\bar{V}),(\bar{V},\bar{V},V),(\bar{V},\bar{V},\bar{V})\} \end{gathered}$$

Els casos favorables són quatre: $(V,V,V)$, $(V,V,\bar{V})$, $(V,\bar{V},V)$, $(\bar{V},V,V)$.

Ara bé, per escollir cada metge en realitat fem un altre experiment compost: escollim aleatòriament un país entre $A$, $F$, $I$, i un cop escollit el metge, aquest pot estar a favor ($V$), o en contra ($\bar{V}$) d'aplicar la vacuna.

Representem el nostre problema en un diagrama en arbre. Hem de tenir clar que aquest experiment ho repetim tres vegades, una per a cada vot. Es tracta d'una votació "amb reposició", ja que el mateix metge pot votar més d'una vegada. D'aquesta manera, la situació és la mateixa per a les tres votacions.

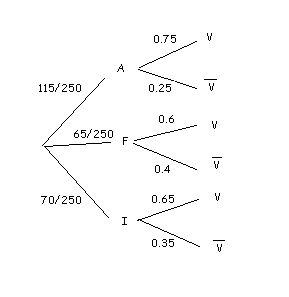
El nostre espai mostral de cada experiment és ${\mathrm{\Omega }}_i=\{(A,V),(A,\bar{V}),(F,V),(F,\bar{V}),(I,V),(I,\bar{V})\}$. Quina és la probabilitat que un metge escollit a l'atzar estigui a favor de la vacuna?

Pel teorema de la probabilitat total,

$$P(V)=P(A)\cdot P(V/A)+P(F)\cdot P(V/F)+P(I)\cdot P(I/F)$$

Vist d'una altra manera, sumem la probabilitat de totes les branques que acaben en $V$.

Substituint, $$P(V)={\displaystyle \frac{115}{250}}\cdot 0,75+{\displaystyle \frac{65}{250}}\cdot 0,6+{\displaystyle \frac{70}{250}}\cdot 0,65=0,345+0,156+0,182=0,683$$

És a dir, una probabilitat del 68,3%. Com sabem que $P(\bar{V})=1-P(V)$, també tenim $P(\bar{V})=1-0,683=0,317$, o el que és el mateix, una probabilitat del 31,7%.

Repetim aquesta elecció tres vegades. Tenim quatre casos favorables:

• Cas $(V,V,V)$: La seva probabilitat és $0,683\cdot 0,683\cdot 0,683=0,319$.
• Cas $(V,V,\bar{V})$: La seva probabilitat és $0,683\cdot 0,683\cdot 0,317=0,148$.
• Cas $(V,\bar{V},V)$: La seva probabilitat és $0,683\cdot 0,317\cdot 0,683=0,148$.
• Cas $(\bar{V},V,V)$: La seva probabilitat és $0,317\cdot 0,683\cdot 0,683=0,148$.

Finalment, la probabilitat de tenir com a mínim dos vots a favor és: $$0,319+0,148+0,148+0,148=0,763$$ és a dir, del 76,3%.

Observació 1:

En aquest el cas que no ens importa l'ordre en que escollim els metges (només si estan a favor o no de la vacuna): podríem considerar que el nostre espai mostral és $\mathrm{\Omega }=\{\{V,V,V\},\{V,V,\bar{V}\},\{V,\bar{V},V\},\{\bar{V},V,V\}\}$, sense tenir en compte l'ordre en què han sortit escollits els metges, sinó tan sols si estan a favor o en contra.

En comptes d'escriure els successos elementals amb parèntesis "( )", els escrivim en aquest cas amb claus "{ }", és la forma de dir que els nostres resultats estan desordenats. Tractarem això amb més profunditat en el tema de combinatòria.

Els casos favorables són dos, en aquest cas: $\{V,V,V\}$ i $\{V,V,\bar{V}\}$, tot i que hem de tenir clar que el segon compta per tres, ja que es correspon en realitat amb tres esdeveniments ordenats. D'aquesta manera, calcularíem de la mateixa manera la probabilitat de cada cas, i obtindríem la probabilitat total fent $P(\text{"com a mínim dos vots a favor"})=P(\{V,V,V\})+3P(\{V,V,\bar{V}\})$, de manera que la probabilitat acaba sortint la mateixa tant si els considerem ordenats com desordenats.

Observació 2:

Pot semblar estrany que en el nostre problema deixem que un metge pugui votar més d'una vegada, seria més realista que un metge només pogués votar com a màxim una vegada. El que passa en realitat és que la probabilitat que això passi és tan petita, que normalment estudiaríem el problema d'aquesta manera, ja que probablement cometem un error més gran aproximant els decimals dels resultats parcials que complicant el problema perquè un metge només pugui votar una vegada. No obstant, és interessant intentar resoldre'l suposant que un metge només pot votar una vegada (llavors hauríem de calcular una probabilitat condicionada diferent per a cada elecció del metge), i comparar-lo amb el resultat que hem trobat.