Regions with verticalcross-sections
This type of region is limited by the interval $$[a, b]$$ in the variable $$x$$, and for certain functions $$g (x)$$, $$h (x)$$ in the variable $$y$$, or in other words $$y\in [g(x),h(x)]$$.
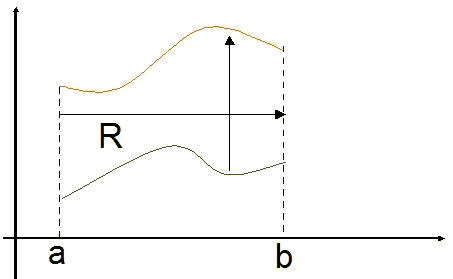
Then,$$$\displaystyle \int_R f(x,y) \ dxdy = \int_a^b\int_{g(x)}^{h(x)} f(x,y) dy dx$$$
Regions with horizontal cross-sections
This type of region is limited by the interval $$[c, d]$$ in the variable $$y$$, and for certain functions $$g(y)$$, $$h(y)$$ in the variable $$x$$, or in other words $$x \in [g(y),h(y)]$$.
Then,$$$\displaystyle \int_R f(x,y) \ dxdy=\int_c^d \int_{g(y)}^{h(y)} f(x,y) \ dxdy$$$
Regions without cross-sections
In the case where the region does not have cross-sections, it is advisable to carry out a change of variable, imposing new variables, that will give us cross-sections.
On the other hand, it is possible that it will be necessary to separate the integral into different parts and that the integration limits have complex expressions.