Regiones con secciones transversales verticales
Este tipo de región está limitada por el intervalo $$[a, b]$$ en la variable $$x$$, y por ciertas funciones $$g (x)$$, $$h (x)$$ en la variable $$y$$, de forma que $$y\in [g(x),h(x)]$$.
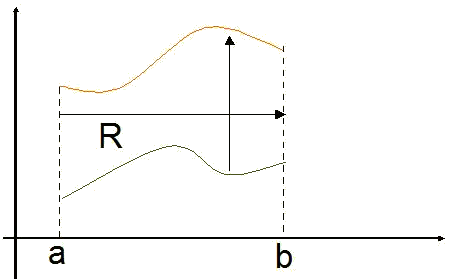
Entonces,$$$\displaystyle \int_R f(x,y) \ dxdy = \int_a^b\int_{g(x)}^{h(x)} f(x,y) dy dx$$$
Regiones con secciones transversales horizontales
Este tipo de región está limitada por el intervalo $$[c, d]$$ en la variable $$y$$, y por ciertas funciones $$g(y)$$, $$h(y)$$ en la variable $$x$$, de forma que $$x \in [g(y),h(y)]$$.
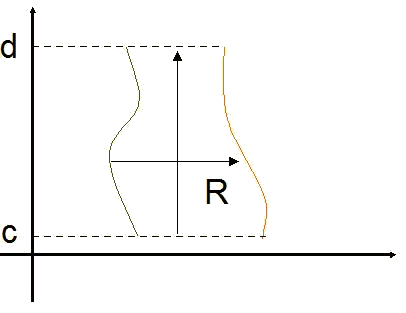
Entonces,$$$\displaystyle \int_R f(x,y) \ dxdy=\int_c^d \int_{g(y)}^{h(y)} f(x,y) \ dxdy$$$
Regiones sin secciones transversales
En el caso en que la región no tenga secciones transversales, es recomendable realizar un cambio de variable a unas nuevas variables que nos den unas secciones transversales.
En caso contrario, es posible que sea necesario separar la integral en trozos y que los límites de integración tengan formas difíciles de operar.