The operations defined for rational numbers can be extended for real numbers.
To introduce the operations for real numbers we need some previous concepts.
An irrational number is formed by a sequence of digits. These digits define successive approximations of the number.
Example
For number
Example
For number
To calculate the operation between two real numbers we use the successive approximations. By computing with the two approximations we obtain the digits of the result.
Example
In order to add
If we use a calculator, we will get the following result
Example
For the subtraction of
If we use a calculator, we obtain that
Example
For the product of
If we use a calculator, we obtain the following result
Example
Finally, we use the same procedure for the quotient of
Using the calculatator
And we observe that the value we obtain gets close to the real one.
Addition of real numbers
Given any two real numbers
The point for number
Properties of the sum
-
Associative Property: given any three real numbers
-
Commutative Property: For any pair of real numbers
-
Neutral Element: There exists a real number,
- Opposite Element: for any real number
All these properties can be summed up by saying that the set
Let's remark that subtracting a real number from another is to add its opposite:
Product of real numbers
If
We can draw the product between two numbers
We start by placing on the real straight line the numbers
We draw an auxiliary straight line that goes through the point
We join, now, the points
The length of the segment
In fact, using the Thales' theorem we get that:
But since we have that
So, translating the length
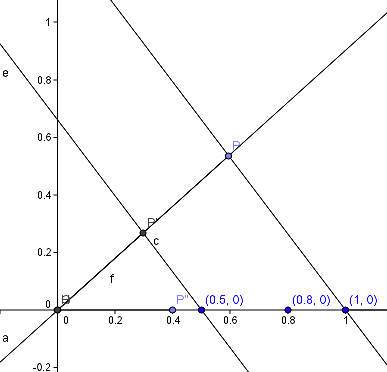
Example
To multiply graphically numbers
We draw an auxiliary straight line that passes through point
We draw the parallel to
Translating the distance
Properties of the product
-
Associative Property: given any three real numbers
-
Commutative Property: For any pair of real numbers
-
Unit element: a real number
- Inverse Element: for any real number
All these properties also define theset of real numbersas an Abelian group with the operation product.
To draw the inverse of
We draw an auxiliary straight line that crosses point
We join
The segment
Indeed, using the Thales' theorem we find out that:
So that to find point
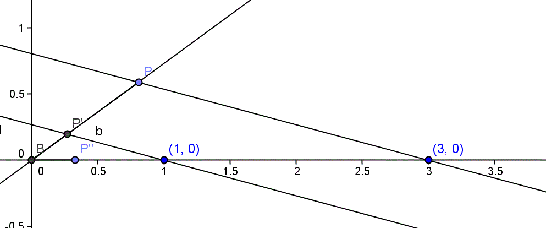
Example
To draw the inverse number of
Now we place on an auxiliary straight line a point
We draw the straight line that joins point
Once we have done this, we will be able to translate the point
We have to point out that all these properties define the set
Furthermore, we can also observe that dividing a real number by another, consists of multiplying it by its inverse:
There also exists a last property related to the sum and the product of real numbers:
- Distributive property of the product regarding the sum: given any three real numbers
