Las operaciones definidas para números racionales pueden extenderse para números reales.
Para presentar las operaciones entre números reales necesitamos algunos conceptos previos.
Un número irracional viene dado por una secuencia de dígitos. Estos dígitos definen aproximaciones sucesivas del número. Veamos algún ejemplo:
Ejemplo
Para al número
Ejemplo
Para el número
Para calcular la operación entre dos números reales utilizamos las aproximaciones sucesivas. Operando las dos aproximaciones obtenemos los dígitos del resultado.
Ejemplo
Para la suma de
Si hacemos el cálculo de esta suma mediante una calculadora obtenemos que
Y observamos que el valor que hemos obtenido con las aproximaciones se acerca al valor de la calculadora.
Ejemplo
Para la resta de
Si calculamos en una calculadora obtenemos que
Ejemplo
Para el producto de
Este cálculo, mediante calculadora, nos da
Ejemplo
Finalmente, para el cociente de
Si calculamos en una calculadora obtenemos que
Y observamos que el valor que obtenemos se va acercando al real.
Suma de números reales
Dados dos números reales cualesquiera
El punto que corresponde al número
Propiedades de la suma
-
Propiedad asociativa: dados tres números reales cualesquiera
-
Propiedad conmutativa: Para todo par de números reales
-
Elemento neutro: existe un número real, el
- Elemento opuesto: para todo número real
Todas estas propiedades, se resumen diciendo que el conjunto
Observemos que restar un número real a otro, consiste en sumar su opuesto:
Producto de números reales
Si
Podemos construir gráficamente el producto entre dos números
Empezamos colocando sobre la recta real los números
Trazamos una recta auxiliar que pase por el punto
Unimos ahora los puntos
La longitud del segmento
Efectivamente, usando el teorema de Tales tenemos que:
Pero al tener que,
Así que trasladando la longitud
Ejemplo
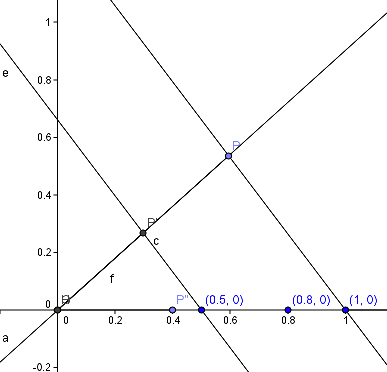
Para multiplicar gráficamente los números
Trazamos una recta auxiliar que pase por
Trazamos la recta paralela a
Trasladando la distancia
Propiedades del producto:
-
Propiedad asociativa: dados tres números reales cualesquiera
-
Propiedad conmutativa: Para todo par de números reales
-
Elemento unidad: existe un número real, el
- Elemento inverso: para todo número real
Observamos que todas estas propiedades también definen el conjunto de números reales como un grupo abeliano con la operación
Para construir gráficamente el inverso de
Trazamos una recta auxiliar por
Sea
Unimos
El segmento
Efectivamente, usando el teorema de Tales tenemos que:
Pero tenemos que
Así que para encontrar el punto
Ejemplo
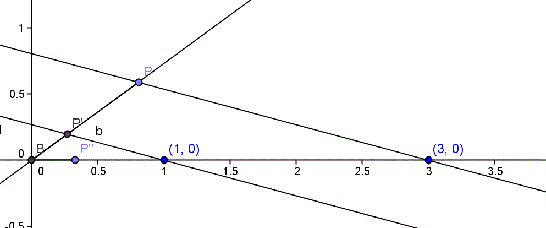
Para dibujar el número inverso de
A continuación marcamos sobre una recta auxiliar un punto
Trazamos la recta que une el punto
Una vez hecho esto, solamente nos queda trasladar el punto
Además, también se da que dividir un número real a otro, consiste en multiplicar su inverso:
Existe también una última propiedad que relaciona la suma y el producto de números reales:
- Propiedad distributiva del producto respecto de la suma: dados tres números reales cualesquiera
