Les operacions definides pels nombres racionals es poden estendre pels nombres reals.
Per presentar les operacions entre nombres reals necessitem alguns conceptes previs.
Un nombre irracional ve donat per una seqüència de dígits. Aquests dígits defineixen aproximacions successives del nombre. Vegem algun exemple:
Exemple
Per al nombre
Exemple
Per al nombre
Per calcular l'operació entre dos nombres reals utilitzem les aproximacions successives. Operant les dues aproximacions obtenim els dígits del resultat. Vegem alguns exemples:
Exemple
Per a la suma de
Si fem el càlcul d'aquesta suma mitjançant una calculadora obtenim que:
I observem que el valor que hem obtingut mitjançant les aproximacions s'apropa al de la calculadora.
Exemple
Per a la resta de
Si ho calculem en una calculadora obtenim que
Exemple
Per al producte de
Aquest càlcul, mitjançant calculadora, ens dóna
Exemple
Finalment, per al quocient de
Si calculem en una calculadora obtenim que
I observem que el valor que obtenim es va acostant al real.
Suma de nombres reals
Donats dos nombres reals qualssevol
El punt que correspon al nombre
Propietats de la suma:
-
Propietat associativa de la suma: donats tres nombres reals qualssevol
-
Propietat commutativa: per a tot parell de nombres reals
-
Element neutre: existeix un nombre real, el
- Element oposat: per a tot nombre real
Totes aquestes propietats, es resumeixen dient que el conjunt
Observem que restar un nombre real a un altre, consisteix a sumar el seu oposat:
Producte de nombres reals
Si
Podem construir gràficament el producte entre dos nombres
Comencem posant sobre la recta real els nombres
Tracem una recta auxiliar que passi pel punt
Unim ara els punts
La longitud del segment
Efectivament, usant el teorema de Tales tenim que:
Però al tenir que,
Així que traslladant la longitud
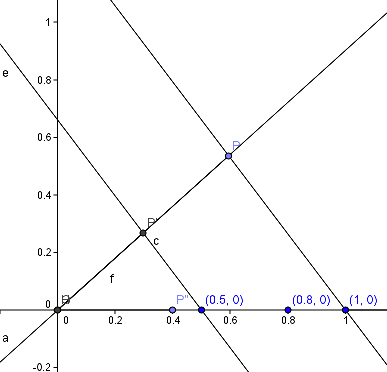
Exemple
Per a multiplicar gràficament els nombres
Tracem una recta auxiliar que passi per
Tracem la recta paral·lela a
Traslladant la distància
Propietats de la multiplicació:
-
Propietat associativa: donats tres nombres reals qualssevol
-
Propietat commutativa: per a tot parell de nombres reals
-
Element unitat: existeix un nombre real, l'
- Element invers: per a tot nombre real
Observem que totes aquestes propietats també ens defineixen el conjunt de nombres reals com un grup abelià amb l'operació
Per construir gràficament l'invers de
Tracem una recta auxiliar per
Sigui
Unim
El segment
Però tenim que
Així que per trobar el punt
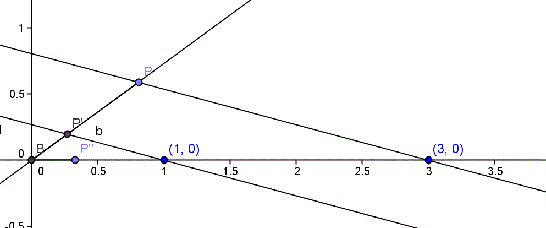
Exemple
Per dibuixar el nombre invers de
A continuació marquem sobre una recta auxiliar un punt
Tracem la recta que uneix el punt
Un cop fet això, només ens queda traslladar el punt
A més a més, també tenim que dividir un nombre real entre un altre, consisteis en multiplicar per l'invers:
Existeix també una última propietat que relaciona la suma i el producte de nombres reals:
- Propietat distributiva del producte respecte de la suma: donats tres nombres reals qualssevol
