When mathematics introduced algebra and polynomials, they did not think they would be such useful tools for solving many problems.
Consider the following figure:
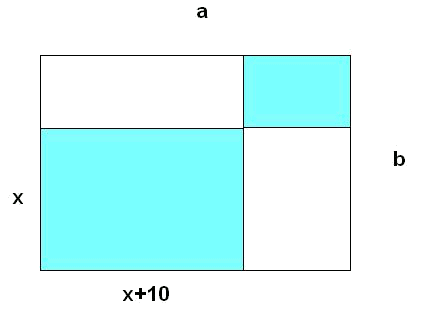
Let $$a$$ be the length of the rectangle, $$b$$ the width of the rectangle and $$x$$ the width of the colored rectangle.
If we know that the colored area is half the area of the entire rectangle, find a polynomial that expresses the above mentioned relation. Use it to solve (i.e., find the value of $$x$$) for the particular case of $$a=b=20$$.
The area of the big rectangle is $$a\cdot b$$
And the colored area is formed by two rectangles:
$$\left.\begin{array}{c} x\cdot(x+10) \\ (a-x-10)\cdot(b-x) \end{array} \right\} = (a-x-10)\cdot(b-x)+x\cdot(x+10)$$
Therefore, we must impose:
$$\dfrac{(a-x-10)\cdot(b-x)+x\cdot(x+10)}{ab}=\dfrac{1}{2}$$
To find a polynomial we develop the previous equation:
$$$2\cdot((a-x-10)\cdot(b-x)+x\cdot(x+10))=ab \Leftrightarrow$$$ $$$2\cdot( a\cdot(b-x)-x\cdot(b-x)-10\cdot(b-x)+x^2+10x)=ab \Leftrightarrow$$$ $$$2\cdot( ab-ax-xb+x^2-10b+10x+x^2+10x)=ab \Leftrightarrow$$$ $$$2\cdot( 2x^2+(20-a-b)x+ab-10b )=ab \Leftrightarrow$$$ $$$4x^2+(40-2a-2b)x+ab-20b=0$$$
We already have the polynomial that we were looking for. Now we consider the particular case of $$a=b=20$$:
$$4x^2+(40-2a-2b)x+ab-20b=0$$
$$\Leftrightarrow 4x^2+(40-2\cdot20-2\cdot20)x+20\cdot20-20\cdot20=0 \Leftrightarrow$$
$$\Leftrightarrow 4x^2-40x=0 \Leftrightarrow 4x(x-10)=0$$
The solutions of the equation are:
$$\left\{\begin{array}{c} x_1=0 \\ x_2=10 \end{array} \right.$$
And the only one that makes sense geometrically is the second one with $$x=10$$.
A football field has unknown dimensions. Nonetheless, a maintenance worker tells us that the relation between the width minus $$20$$ metres is equal to one half. Also, the sum of the length and the width is $$170$$ meters. What are the dimensions of the field?
We will use variable $$x$$ to denote the "width of the field", and the variable $$y$$ to denote the "length of the field". And so, according to the exercise, we would have the following equations:
$$$\dfrac{x}{y-20}=\dfrac{1}{2}$$$ $$$x+y=170$$$ From the second equality we obtain: $$$x=170-y$$$ And replacing it in the first equality and developing the expression: $$$\dfrac{170-y}{y-20}=\dfrac{1}{2} \Leftrightarrow 2\cdot(170-y)=1\cdot(y-20) \Leftrightarrow 340-2y=y-20 \Leftrightarrow$$$ $$$\Leftrightarrow y=\dfrac{360}{3}=120$$$ Therefore: $$$x=170-120=50$$$ And so, the dimensions of the football ground will be $$120$$ meters long and $$50$$ meters wide.
Demonstrate that if the square of the sum two numbers is equal to the sum of the squares of the stated numbers, one of these numbers is zero.
We will denote by $$x$$ the first number, and by $$y$$ the second number. And so, according to the statement, we must impose: $$$(x+y)^2=x^2+y^2$$$ According to the algebraic identities, we develop the first factor: $$$(x+y)^2=x^2+2xy+y^2=x^2+y^2$$$ Now we can simplify the squares, and we are left with the term $$2xy=0$$. This will be satisfied if some of the values is zero. And so, $$$x=0 \ \mbox{or} \ y=0$$$
Let's consider a rectangle to be that of the figure below:
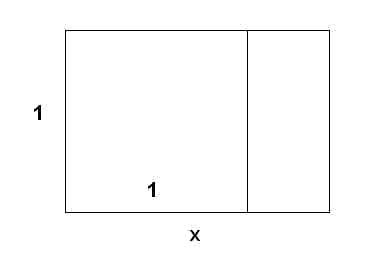
If we know that the quotient between the height and the width is equal to the value of the width minus one, find the value of the width of the rectangle.
We identify, as in the figure, the width with the variable $$x$$. Therefore, if we write down the relation between the sides we obtain: $$$\dfrac{1}{x}=x-1$$$ If we develop: $$$\dfrac{1}{x}=x-1 \Leftrightarrow 1=x\cdot(x-1)=x^2-x \Leftrightarrow x^2-x-1=0$$$ Now, we only need to apply the formula to solve quadratic equations:
$$x=\dfrac{1\pm\sqrt{(-1)^2+4\cdot1\cdot1}}{2}=\dfrac{1+\sqrt{5}}{2}=\left\{\begin{array}{c} x_1=\dfrac{1+\sqrt{5}}{2}\simeq1,61\ldots \\ x_2=\dfrac{1-\sqrt{5}}{2}\simeq-0,61\ldots \end{array} \right.$$
Obviously, we take the positive solution since the negative one does not make sense.
Therefore, the length of the rectangle is $$1,61\ldots$$
Finally, it is worth knowing that the solutions to the equation seen in this example are called the Golden Number, a value that has many different mathematic and historical curiosities as well as very interesting properties.