Cuando los matemáticos introdujeron el álgebra y los polinomios, no pensaban que podrían ser herramientas muy útiles para la resolución de infinidad de problemas.
Consideramos la figura siguiente:
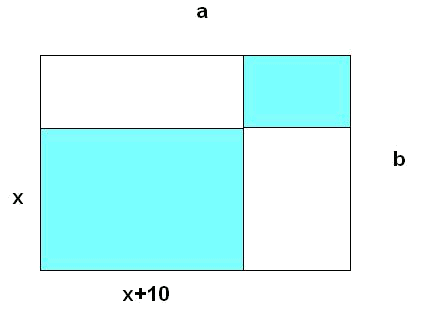
Sean $$a$$ la longitud del rectángulo, $$b$$ la anchura del rectángulo y $$x$$ la anchura del rectángulo colorido.
Si se sabe que el área colorida es la mitad que el área total del rectángulo, encontrar una expresión polinómica que exprese dicha relación. Solucionarla (encontrar el valor de $$x$$) para el caso particular de $$a=b=20$$.
El área del rectángulo grande es $$a\cdot b$$
Y el área colorida está formada por dos rectángulos vale:
$$\left.\begin{array}{c} x\cdot(x+10) \\ (a-x-10)\cdot(b-x) \end{array} \right\} = (a-x-10)\cdot(b-x)+x\cdot(x+10)$$
Por lo tanto, debemos imponer:
$$\dfrac{(a-x-10)\cdot(b-x)+x\cdot(x+10)}{ab}=\dfrac{1}{2}$$
Para encontrar una expresión polinómica desarrollamos la ecuación anterior:
$$$2\cdot((a-x-10)\cdot(b-x)+x\cdot(x+10))=ab \Leftrightarrow$$$ $$$2\cdot( a\cdot(b-x)-x\cdot(b-x)-10\cdot(b-x)+x^2+10x)=ab \Leftrightarrow$$$ $$$2\cdot( ab-ax-xb+x^2-10b+10x+x^2+10x)=ab \Leftrightarrow$$$ $$$2\cdot( 2x^2+(20-a-b)x+ab-10b )=ab \Leftrightarrow$$$ $$$4x^2+(40-2a-2b)x+ab-20b=0$$$
Ya tenemos la expresión polinómica que buscábamos. Ahora consideramos el caso particular de $$a=b=20$$:
$$4x^2+(40-2a-2b)x+ab-20b=0$$
$$\Leftrightarrow 4x^2+(40-2\cdot20-2\cdot20)x+20\cdot20-20\cdot20=0 \Leftrightarrow$$
$$\Leftrightarrow 4x^2-40x=0 \Leftrightarrow 4x(x-10)=0$$
Las soluciones de la ecuación son:
$$\left\{\begin{array}{c} x_1=0 \\ x_2=10 \end{array} \right.$$
Y la única que tiene sentido geométrico es la segunda, $$x=10$$.
Un campo de fútbol tiene medidas desconocidas. Con todo, un operario de mantenimiento nos cuenta que la relación entre lo ancho y lo largo menos $$20$$ metros es igual a un medio. Asimismo, la suma de lo largo y lo ancho es de $$170$$ metros. Cúales son las medidas del campo de fútbol?
Indentificamos la incógnita "ancho del campo" con la variable $$x$$, y la incógnita "largo del campo" con la variable $$y$$. Así pues, según el enunciado, tendríamos las ecuaciones siguientes:
$$$\dfrac{x}{y-20}=\dfrac{1}{2}$$$ $$$x+y=170$$$ De la segunda igualdad obtenemos: $$$x=170-y$$$ Y sustituyéndolo en la primera igualdad y desarrollando: $$$\dfrac{170-y}{y-20}=\dfrac{1}{2} \Leftrightarrow 2\cdot(170-y)=1\cdot(y-20) \Leftrightarrow 340-2y=y-20 \Leftrightarrow$$$ $$$\Leftrightarrow y=\dfrac{360}{3}=120$$$ Por lo tanto: $$$x=170-120=50$$$ Así pues, las medidas del campo de fútbol serán $$120$$ metros de largo y $$50$$ metros de ancho.
Demostrar que si el cuadrado de la suma dos números es igual a la suma de los cuadrados de dichos números, alguno de estos números es cero.
Indentificamos el primer número con la variable $$x, y$$ el segundo número con la variable $$y$$. Así pues, según el enunciado, debemos imponer: $$$(x+y)^2=x^2+y^2$$$ Según las identidades notables, desarrollamos el primer factor: $$$(x+y)^2=x^2+2xy+y^2=x^2+y^2$$$ Ahora podemos simplificar los cuadrados, y nos queda el término $$2xy=0$$. Esto se cumplirá si alguno de los valores es cero. Así pues, $$$x=0 \ \mbox{ó} \ y=0$$$
Consideremos un rectángulo como el de la figura:
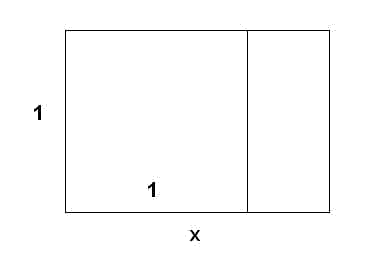
Se conoce que el cociente entre la altura y la anchura es igual al valor de la anchura menos uno. Encontrar el valor de la anchura del rectángulo.
Identificamos, tal y como ya nos anticipa el dibujo, la anchura con la variable $$x$$. Por lo tanto, si explicitamos la relación entre los lados en una ecuación: $$$\dfrac{1}{x}=x-1$$$ Si desarrollamos: $$$\dfrac{1}{x}=x-1 \Leftrightarrow 1=x\cdot(x-1)=x^2-x \Leftrightarrow x^2-x-1=0$$$ Ahora sólo hace falta aplicar la expresión para solucionar ecuaciones cuadráticas:
$$x=\dfrac{1\pm\sqrt{(-1)^2+4\cdot1\cdot1}}{2}=\dfrac{1+\sqrt{5}}{2}=\left\{\begin{array}{c} x_1=\dfrac{1+\sqrt{5}}{2}\simeq1,61\ldots \\ x_2=\dfrac{1-\sqrt{5}}{2}\simeq-0,61\ldots \end{array} \right.$$
Evidentemente, tomamos la solución positiva ya que la negativa no tiene sentido para un ente geométrico.
Por lo tanto, la longitud de dicho rectángulo es de $$1,61\ldots$$
Finalmente, reseñar que las soluciones de la ecuación planteada corresponden a los valores del Número de Oro, un valor que aparece en infinitud de curiosidades matemáticas y que tiene propiedades muy interesantes.
