Quan els matemàtics van introduir l'àlgebra i els polinomis, no pensaven que podrien ser eines molt útils per a la resolució d'infinitat de problemes.
Considerem la figura següent:
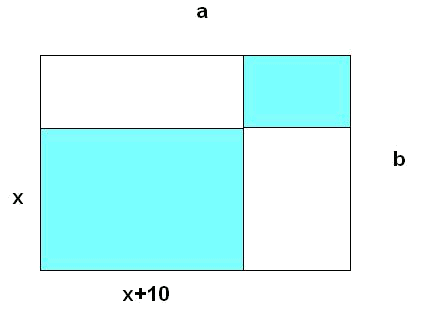
Siguin $$a$$ la longitud del rectangle, $$b$$ l'amplada del rectangle i $$x$$ l'amplada del rectangle colorit.
Si se sap que l'àrea acolorida és la meitat que l'àrea total del rectangle, trobar una expressió polinòmica que expressi aquesta relació. Solucionar (trobar el valor de $$x$$) per al cas particular de $$a=b=20$$.
L'àrea del rectangle gran és $$a\cdot b$$
I l'àrea acolorida està formada per dos rectangles val:
$$\left.\begin{array}{c} x\cdot(x+10) \\ (a-x-10)\cdot(b-x) \end{array} \right\} = (a-x-10)\cdot(b-x)+x\cdot(x+10)$$
Per tant, hem d'imposar:
$$\dfrac{(a-x-10)\cdot(b-x)+x\cdot(x+10)}{ab}=\dfrac{1}{2}$$
Per trobar una expressió polinòmica desenvolupem l'equació anterior:
$$$2\cdot((a-x-10)\cdot(b-x)+x\cdot(x+10))=ab \Leftrightarrow$$$ $$$2\cdot( a\cdot(b-x)-x\cdot(b-x)-10\cdot(b-x)+x^2+10x)=ab \Leftrightarrow$$$ $$$2\cdot( ab-ax-xb+x^2-10b+10x+x^2+10x)=ab \Leftrightarrow$$$ $$$2\cdot( 2x^2+(20-a-b)x+ab-10b )=ab \Leftrightarrow$$$ $$$4x^2+(40-2a-2b)x+ab-20b=0$$$
Ja tenim l'expressió polinòmica que buscàvem. Ara considerem el cas particular de $$a=b=20$$:
$$4x^2+(40-2a-2b)x+ab-20b=0$$
$$\Leftrightarrow 4x^2+(40-2\cdot20-2\cdot20)x+20\cdot20-20\cdot20=0 \Leftrightarrow$$
$$\Leftrightarrow 4x^2-40x=0 \Leftrightarrow 4x(x-10)=0$$
Les solucions de l'equació són:
$$\left\{\begin{array}{c} x_1=0 \\ x_2=10 \end{array} \right.$$
I l'única que té sentit geomètric és la segona, $$x=10$$.
Un camp de futbol té mesures desconegudes. Amb tot, un operari de manteniment ens explica que la relació entre l'ample i llarg menys $$20$$ metres és igual a un mig. Així mateix, la suma de llarg i l'ample és de $$170$$ metres. Quins són les mesures del camp de futbol?
Identificant la incògnita "ample del camp" amb la variable $$x$$, i la incògnita "llarg del camp" amb la variable $$y$$. Així doncs, segons l'enunciat, tindríem les equacions següents:
$$$\dfrac{x}{y-20}=\dfrac{1}{2}$$$ $$$x+y=170$$$ De la segona igualtat obtenim: $$$x=170-y$$$ I substituint a la primera igualtat i desenvolupant: $$$\dfrac{170-y}{y-20}=\dfrac{1}{2} \Leftrightarrow 2\cdot(170-y)=1\cdot(y-20) \Leftrightarrow 340-2y=y-20 \Leftrightarrow$$$ $$$\Leftrightarrow y=\dfrac{360}{3}=120$$$ Per tant: $$$x=170-120=50$$$ Així doncs, les mesures del camp de futbol seran $$120$$ metres de llarg i $$50$$ metres d'ample.
Demostrar que si el quadrat de la suma de dos números és igual a la suma dels quadrats d'aquests números, algun d'aquests números és zero.
Identificant el primer número amb la variable $$x$$ i el segon número amb la variable $$y$$. Així doncs, segons l'enunciat, hem d'imposar: $$$(x+y)^2=x^2+y^2$$$ Segons les identitats notables, desenvolupem el primer factor: $$$(x+y)^2=x^2+2xy+y^2=x^2+y^2$$$ Ara podem simplificar els quadrats, i ens queda el terme $$2xy=0$$. Això es complirà si algun dels valors és zero. Així doncs, $$$x=0 \ \mbox{o} \ y=0$$$
Considerem un rectangle com el de la figura:
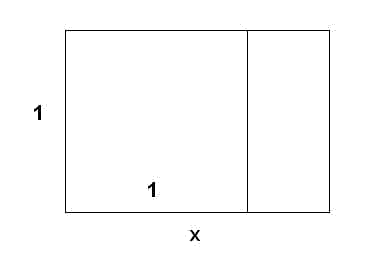
Es coneix que el quocient entre l'altura i l'amplada és igual al valor de l'amplada menys un. Trobar el valor de l'amplada del rectangle.
Identifiquem, tal com ja ens anticipa el dibuix, l'amplada amb la variable $$x$$. Per tant, si explicitem la relació entre els costats en una equació: $$$\dfrac{1}{x}=x-1$$$ Si desenvolupem: $$$\dfrac{1}{x}=x-1 \Leftrightarrow 1=x\cdot(x-1)=x^2-x \Leftrightarrow x^2-x-1=0$$$ Ara només cal aplicar l'expressió per solucionar equacions quadràtiques:
$$x=\dfrac{1\pm\sqrt{(-1)^2+4\cdot1\cdot1}}{2}=\dfrac{1+\sqrt{5}}{2}=\left\{\begin{array}{c} x_1=\dfrac{1+\sqrt{5}}{2}\simeq1,61\ldots \\ x_2=\dfrac{1-\sqrt{5}}{2}\simeq-0,61\ldots \end{array} \right.$$
Evidentment, prenem la solució positiva ja que la negativa no té sentit per a un ens geomètric.
Per tant, la longitud d'aquest rectangle és de $$1,61\ldots$$
Finalment, ressenyar que les solucions de l'equació plantejada corresponen als valors del número d'Or, un valor que apareix en infinitut de curiositats matemàtiques i que té propietats molt interessants.