The dodecahedron is a regular polyhedron of $$12$$ faces. If the mentioned faces are regular pentagons we call it a regular dodecahedron:
To find the area of edge a of a dodecahedron $$a=10 \ m$$.
To calculate the area of edge $$a$$ of the regular dodecahedron it will be necessary to first find the area of side $$a$$ of a regular pentagon.
We need to use trigonometry to find the area of the pentagon from $$a$$. This can be very useful, since $$a$$ will not be a regular occurrence in problems like finding the area of a pentagon, or a dodecahedron.
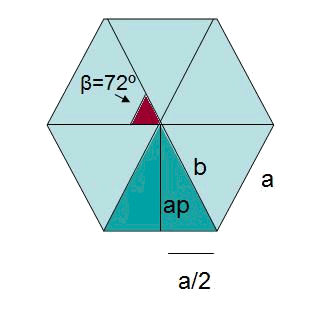
The five triangles with height $$ap$$ that compose the pentagon are equal, $$$A_{pentagon}=5 \cdot (\dfrac{a \cdot ap}{2}) \\ b^2=ap^2+\Big(\dfrac{a}{2}\Big)^2$$$ We have to, first, find $$b$$. As, $$\beta=\dfrac{360^\circ}{5}=72^\circ$$ and using the definition of the sinus of the triangle, $$$\sin \dfrac{\beta}{2}=\sin 36^\circ= \dfrac{opposite}{hypotenuse}=\dfrac{\dfrac{a}{2}}{b} \\ b=\dfrac{5}{\sin 36^\circ}= 8,5 \ m \\ 8,5^2=ap^2+5^2 \\ ap= 6,9 \ m$$$
Then, $$$A_{pentagon}=5 \cdot \dfrac{10 \cdot 6,9}{2}= 172 \ m^2 \\ A_{dodecahedron}= 2063,5 \ m^2$$$
Finally, the following expressions allow us to find the area and volume of the dodecahedron of edge $$a$$: $$$A=30 \cdot a \cdot ap \\ V=\dfrac{1}{4}(15+7\sqrt{5})a^3$$$

