El dodecaedro es un poliedro de $$12$$ caras. Si dichas caras son pentágonos regulares se podrá hablar de un dodecaedro regular. Véase la siguiente figura:
Encontrar el área de un dodecaedro de arista $$a=10 \ m$$.
Para calcular el área del dodecaedro regular de arista $$a$$ será necesario encontrar primero el área de un pentágono regular de lado $$a$$.
Será necesario utilizar la trigonometría para encontrar el área del pentágono a partir de $$a$$. Esto puede ser muy útil, ya que $$ap$$ no será un dato habitual en problemas como encontrar el área de un pentágono, o de un dodecaedro.
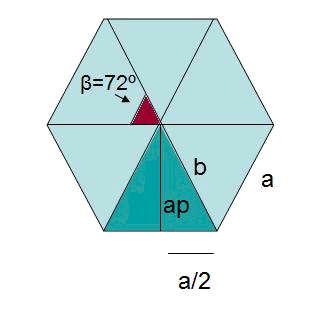
Puesto que los cinco triángulos de altura $$ap$$ que componen el pentágono son iguales, $$$A_{pentágono}=5 \cdot (\dfrac{a \cdot ap}{2}) \\ b^2=ap^2+\Big(\dfrac{a}{2}\Big)^2$$$ Se procede a buscar $$b$$. Sabiendo que, $$\beta=\dfrac{360^\circ}{5}=72^\circ$$ Y utilizando la definición del seno en el triángulo formado por $$ap$$, $$b$$, y $$\dfrac{a}{2}$$ $$$\sin \dfrac{\beta}{2}=\sin 36^\circ= \dfrac{opuesto}{hipotenusa}=\dfrac{\dfrac{a}{2}}{b} \\ b=\dfrac{5}{\sin 36^\circ}= 8,5 \ m \\ 8,5^2=ap^2+5^2 \\ ap= 6,9 \ m$$$
Así pues, $$$A_{pentágono}=5 \cdot \dfrac{10 \cdot 6,9}{2}= 172 \ m^2 \\ A_{dodecaedro}= 2063,5 \ m^2$$$
Finalmente, las siguientes expresiones permiten encontrar el área y el volumen del dodecaedro de arista $$a$$: $$$A=30 \cdot a \cdot ap \\ V=\dfrac{1}{4}(15+7\sqrt{5})a^3$$$

