El dodecàedre és un políedre de $$12$$ cares. Si aquestes cares són pentàgons regulars es podrà parlar d'un dodecàedre regular. Vegeu la figura següent:
Trobar l'àrea d'un dodecàedre d'aresta $$a=10 \ m$$.
Per calcular l'àrea del dodecaedre regular d'aresta $$a$$ serà necessari trobar primer l'àrea d'un pentàgon regular de costat $$a$$ .
Serà necessari utilitzar la trigonometria per trobar l'àrea del pentàgon a partir de $$a$$. Això pot ser molt útil, ja que $$ap$$ no serà una dada habitual en problemes com trobar l'àrea d'un pentàgon, o d'un dodecàedre.
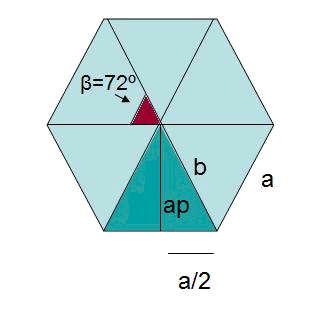
Com que els cinc triangles d'altura $$ap$$ que componen el pentàgon són iguals, $$$A_{pentàgon}=5 \cdot (\dfrac{a \cdot ap}{2}) \\ b^2=ap^2+\Big(\dfrac{a}{2}\Big)^2$$$ Es procedeix a cercar $$b$$. Sabent que, $$\beta=\dfrac{360^\circ}{5}=72^\circ$$ i utilitzant la definició del sinus en el triangle format per $$ap$$, $$b$$, i $$\dfrac{a}{2}$$ $$$\sin \dfrac{\beta}{2}=\sin 36^\circ= \dfrac{oposat}{hipotenusa}=\dfrac{\dfrac{a}{2}}{b} \\ b=\dfrac{5}{\sin 36^\circ}= 8,5 \ m \\ 8,5^2=ap^2+5^2 \\ ap= 6,9 \ m$$$
Així, $$$A_{pentàgon}=5 \cdot \dfrac{10 \cdot 6,9}{2}= 172 \ m^2 \\ A_{dodecàedre}= 2063,5 \ m^2$$$
Finalment, les següents expressions permeten trobar l'àrea i volum del dodecàedre d'aresta $$a$$: $$$A=30 \cdot a \cdot ap \\ V=\dfrac{1}{4}(15+7\sqrt{5})a^3$$$