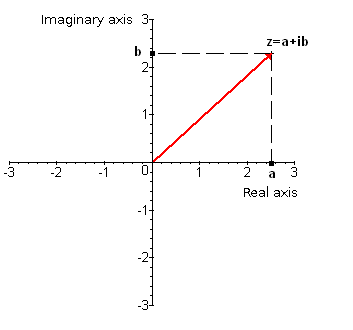
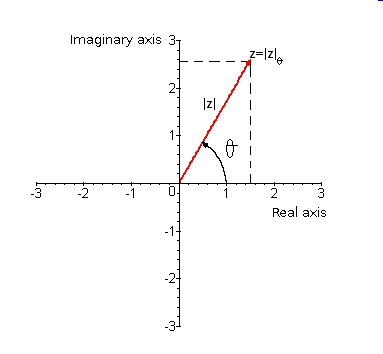Given a complex number $$z$$ we have two ways of represent it. It is possible to have:
- Binomic form: given a complex number its binomic form is the most usual one, $$z=a+bi$$, and it is also possible to identify it with a pair of numbers given in Cartesian coordinates. This pair is $$(a, b)$$ and they allow us to draw $$z$$ in the complex plane. The procedure is as follows:
- Draw the first component of the pair on the axis OX (eix real) (real axis). This is the real part of $$z$$.
- Draw the second component of the pair on the axis OY (imaginary axis). This is the imaginary part of $$z$$.
- Mark the point where the straight lines parallel to the axes OX and OY, and going through $$a$$ and $$b$$, intersect.
-
Join the origin of the complex plane with this point. This is the complex number $$z$$.
-
Polar form: The complex number written in polar form is $$z=|z|_{\alpha}$$ and it is identified by the pair $$(|z|,\alpha)$$ which are its polar coordinates. They will also allow us to draw the number in the complex plane. The procedure is:
- Draw an angle $$\alpha$$ that starts from the origin of the complex plane.
- Take the module of $$z$$, $$|z|$$, draw it. This length is the one that determines the number $$z$$ in the complex plane.