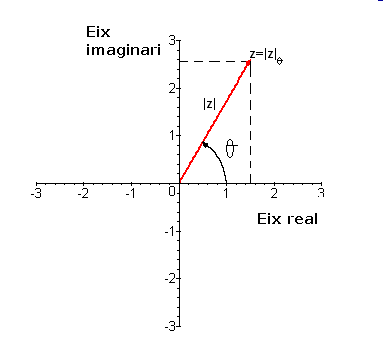Donat un nombre complex $$z$$ es poden considerar les seves dues maneres de representació que se sap fins ara. Així doncs, es pot tenir:
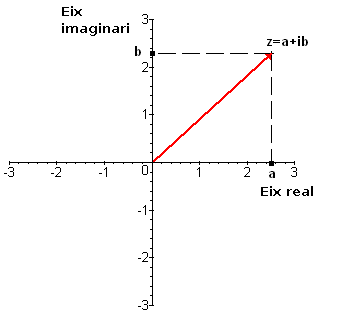
- Forma binòmica: donat un complex en forma binòmica $$z=a+bi$$ també se'l pot identificar amb un parell ordenat al qual anomenarem coordenades cartesianes. Aquest parell és
$$(a, b)$$ i ens permet dibuixar $$z$$ en el pla complex. Repassem-ne el procediment:
- Dibuixar en l'eix OX (eix real) la primera component del parell ordenat. És a dir, la part real de $$z$$.
- Dibuixar en l'eix OY (eix imaginari) la segona component del parell ordenat. És a dir, la part imaginària de $$z$$.
- Marcar el punt on es troben les rectes paral·leles als eixos OX i OY que passen per $$a$$ i $$b$$.
- Unir l'origen del pla complex amb el punt marcat. Aquest és el nombre complex $$z$$.
-
Forma polar: El nombre complex donat en forma polar $$z=|z|_{\alpha}$$ es pot identificar amb el parell $$(|z|,\alpha)$$ que son les seves coordenades polars que permetran dibuixar $$z$$ en el pla complex. El procediment és:
- Dibuixar un angle $$\alpha$$ que surti de l'origen del pla complex.
- Agafar el mòdul de $$z$$, és a dir $$|z|$$, i posar-lo a sobre de l'angle. Aquesta longitud és la que ens determina el nombre $$z$$ en el pla complex.