Representació de nombres complexos en el pla

Ara que sabem treballar amb els nombres complexos i les operacions bàsiques de suma, resta, multiplicació i divisió, anem a introduir-nos en la representació d'aquests números en el pla complex. Per als nombres reals, dibuixàvem una recta i els anàvem posant ordenadament, és a dir:

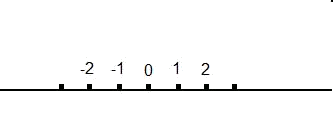
imagen

Per representar gràficament un nombre complex, hem de dibuixar en el pla complex. Aquest està format per un eix real i un eix imaginari. Sobre l'eix real representarem la part real del nombre complex, mentre que en l'eix imaginari representarem la part imaginària. Aquests eixos els dibuixarem perpendiculars i secants en el zero, que té part real i imaginària nula.

Exemple

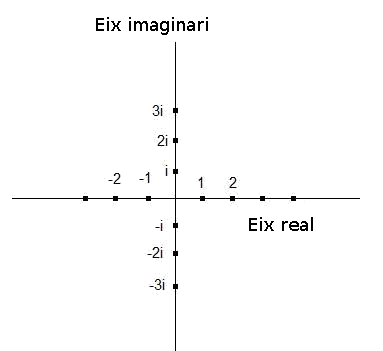
Vegem un exemple del pla complex: imagen

Un nombre complex $z$ en forma binòmica es representarà llavors en un pla complex com l'anterior de la següent manera:

Tenim el complex $z = a + b i$ on:

$a$ és qualsevol nombre real i se l'anomena part real de $z$ .
$b$ és qualsevol nombre real i se l'anomena la part imaginària de $z$ .

Així per a representar un $z = a + b i$ es dibuixa el pla del vector associat a $z$ que és el vector amb origen $(0, 0)$ i extrem el punt $(a, b)$ .

És a dir, es pren la part real del complex i es dibuixa en l'eix real. Es pren la part imaginària i es dibuixa en l'eix imaginari. Es tracen paral·leles als eixos que passen per cada un dels punts marcats i la intersecció d'aquestes paral·leles és el nombre que volíem representar.

imagen

Exemple

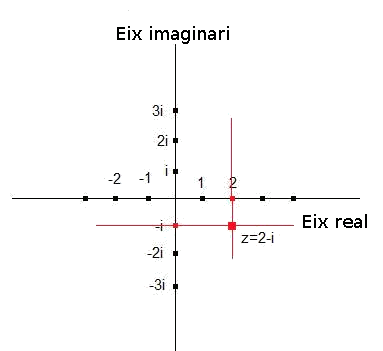
Si volem representar l'imaginari $z = 2 - i$ .

Primer hem de marcar en l'eix real el $2$ .

Després hem de marcar en l'eix imaginari el $- i$ .

Tracem dues rectes:

Una paral·lela a l'eix real que passi pel punt $- i$ .
Una paral·lela a l'eix imaginari que passi pel punt $2$ .

El punt intersecció d'aquestes dues rectes és el nombre $z$ que volíem dibuixar.

Gràficament és:

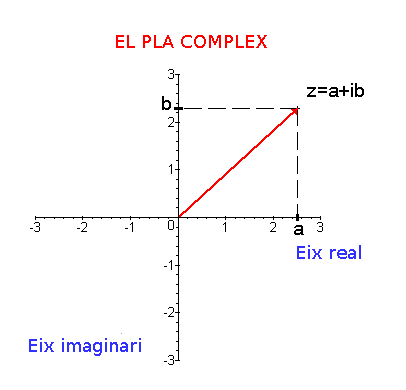
imagen

En definitiva el que estem fent és que a cada nombre complex que ve donat per la forma $z = a + b i$ li associem un vector en el pla que és exactament el vector $(a, b)$ .

Exemple

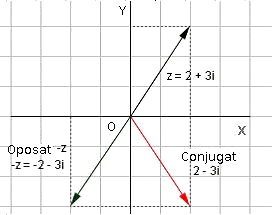
Per exemple, el complex $3 + 9 i$ és l'associat al vector del pla $(3, 9)$ i el complex $- 5 i$ és l'associat al vector $(0, - 5)$ .

Anteriorment hem dit que:

Es defineix el conjugat d'un nombre imaginari com el nombre $\bar{z} = a - i b$ , en aquest cas, per representar prendrem el vector associat $(a, - b)$ .

L'oposat d'un nombre imaginari és $z_{o p} = - z = - a - b i$ , que tindrà vector associat el $(- a, - b)$ .

I l'invers d'un nombre complex és $z^{- 1} = \frac{a}{a^{2} + b^{2}} - \frac{b}{a^{2} + b^{2}} i$ que tindrà vector associat el $(\frac{a}{a^{2} + b^{2}}, - \frac{b}{a^{2} + b^{2}})$ .

Si els dibuixem en el pla complex aquests queden:

imagen