Representación de números complejos en el plano

Ahora que sabemos trabajar con los números complejos y las operaciones básicas de suma, resta, multiplicación y división, vamos a introducirnos en la representación de dichos números en el plano complejo. Para los números reales, dibujábamos una recta y los íbamos colocando ordenadamente, es decir:

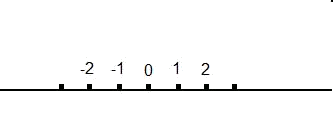
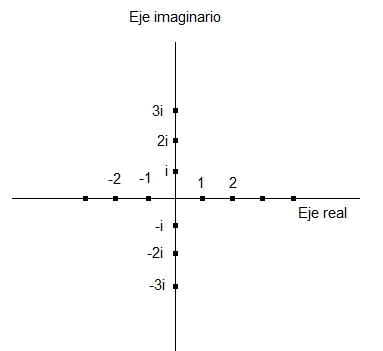
imagen

Para representar gráficamente un número complejo, debemos dibujarlos en el plano complejo. Éste está formado por un eje real y un eje imaginario. Sobre el eje real representaremos la parte real del número complejo, mientras que en el eje imaginario representaremos la parte imaginaria. Dichos ejes los dibujaremos perpendiculares y secantes en el cero, que tiene parte real e imaginaria nula.

Ejemplo

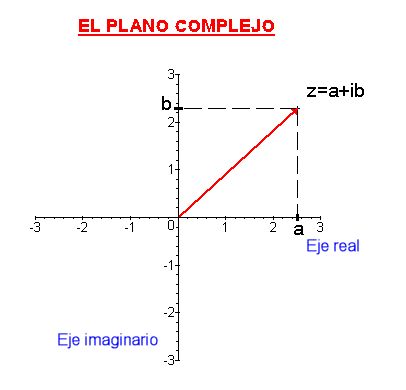
Veamos un ejemplo del plano complejo: imagen

Un número complejo $z$ en forma binómica se representará entonces en un plano complejo como el anterior de la siguiente forma:

Tenemos el complejo $z = a + b i$ donde:

$a$ es cualquier número real, y se le llama parte real de $z$ .
$b$ es cualquier número real, y se le llama la parte imaginaria de $z$ .

Así, para representar un $z = a + b i$ se dibuja en el plano el vector asociado a $z$ que es el vector con origen $(0, 0)$ y extremo el punto $(a, b)$ .

Es decir, se toma la parte real del complejo y se dibuja en el eje real. Se toma la parte imaginaria y se dibuja en el eje imaginario. Se trazan paralelas a los ejes que pasen por cada uno de los puntos marcados y la intersección de dichas paralelas es el número que queríamos representar.

imagen

Ejemplo

Por ejemplo, si queremos representar el imaginario $z = 2 - i$ .

Primero marcamos en el eje real el $2$ .

Luego marcamos en el eje imaginario el $- i$ .

Trazamos dos rectas:

una paralela al eje real que pase por el punto $- i$ .
una paralela al eje imaginario que pase por el punto $2$ .

El punto intersección de estas dos rectas es el número $z$ que queríamos dibujar.

Gráficamente es:

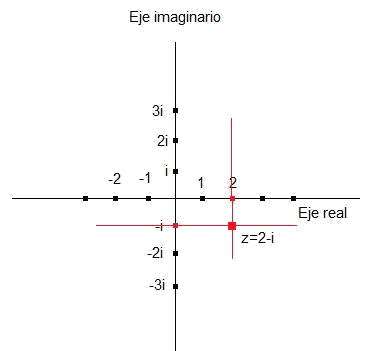
imagen

En definitiva lo que estamos haciendo es que a cada número complejo que viene dado por la forma $z = a + b i$ le asociamos un vector en el plano que es exactamente el vector $(a, b)$ .

Ejemplo

Por ejemplo, el complejo $3 + 9 i$ es el asociado al vector del plano $(3, 9)$ y el complejo $- 5 i$ es el asociado al vector $(0, - 5)$ .

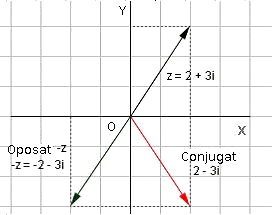
Anteriormente hemos dicho que:

Se define el conjugado de un número imaginario como el número $\bar{z} = a - i b$ , en este caso, para representarlo tomaremos el vector asociado $(a, - b)$ .

El opuesto de un número imaginario es $z_{o p} = - z = - a - b i$ , que tendrá vector asociado el $(- a, - b)$ .

Y el inverso de un número complejo es $z^{- 1} = \frac{a}{a^{2} + b^{2}} - \frac{b}{a^{2} + b^{2}} i$ que tendrá vector asociado el $(\frac{a}{a^{2} + b^{2}}, - \frac{b}{a^{2} + b^{2}})$ .

Si los dibujamos en el plano complejo estos quedan:

imagen