Números complejos en forma polar: modulo y argumento

Hasta ahora hemos aprendido a trabajar con la forma binómica de los números complejos y hemos dado los pasos a seguir para representarlos en el plano complejo.

Lo que hacíamos era adjudicar un vector a cada número complejo, que determinábamos según sus partes real e imaginaria. Así pues, en el fondo estábamos representando vectores en el plano.

Pero los vectores en el plano pueden ser entendidos también como una longitud y un ángulo que los separa del eje horizontal. Por eso, los números imaginarios también se pueden entender como una longitud (que será el módulo) y un ángulo. Veamos cómo se construye.

Para representar un número complejo $z$ n forma polar se deben considerar el módulo y el argumento de éste. El módulo se refiere a la longitud del vector que lo representa en el plano, y el argumento se refiere al ángulo que forma con el eje horizontal.

Es decir, gráficamente sería:

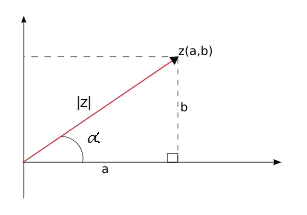
imagen

Así, se tendrá que lo representaremos mediante un módulo y un argumento que escribiremos de la siguiente forma $z = | z |_{α}$ donde:

a $| z |$ se le llama módulo y es la raíz cuadrada de la suma de los cuadrados de la componente real y la componente imaginaria. Se suele escribir $| z |$ o $r$ y se puede pensar como la distancia desde el origen hasta el número complejo $z$ si lo tenemos representado en el plano complejo. Así pues, se tiene: $| z | = | a + b i | = \sqrt{a^{2} + b^{2}}$
a $α$ se le llama el argumento del número complejo $z$ y es el ángulo que forma el número complejo $z$ on el eje real (en sentido positivo) si lo tenemos representado en el plano complejo. Así pues, se tiene: $α = \arctan (\frac{b}{a})$

Se tiene entonces que el argumento de un número complejo no es único, puesto que la expresión $α = \arctan (\frac{b}{a})$ no determina unívocamente el argumente de un número, puesto que hay infinitos ángulos que cumplen la igualdad.

Ahora bien, si restringimos el valor de $α$ para $0 ⩽ α < 2 π$ , hay dos ángulos que difieren en $π$ tienen la misma tangente. Para saber cuál de ellos es el argumento, tendremos en cuenta los signos de $a$ y $b$ , de esta forma conseguiremos saber en que cuadrante está situado el vector del número complejo. Y nos dará el ángulo que buscamos.

Si la parte real y la imaginaria son positivas, el complejo vive en el primer cuadrante.

Ejemplo

Por ejemplo $5 + 9 i$ .

Si la parte real es negativa y la imaginaria es positiva, el complejo vive en el segundo cuadrante.

Ejemplo

Por ejemplo $- 5 + 9 i$ .

Si la parte real y la imaginaria son negativas, el complejo vive en el tercer cuadrante.

Ejemplo

Por ejemplo $- 5 - 9 i$ .

Si la parte real es positiva y la imaginaria es negativa, el complejo vive en el cuarto cuadrante.

Ejemplo

Por ejemplo $5 - 9 i$ .

Ejemplo

Vamos a calcular el módulo y argumento del número $z = 4 + 4 \sqrt{3} i$ .

El complejo $4 + 4 \sqrt{3} i$ tiene por módulo: $| 4 + 4 \sqrt{3} i | = \sqrt{4^{2} + (4 \sqrt{3})^{2}} = \sqrt{16 + 16 \cdot 3} = \sqrt{16 + 48} = \sqrt{64} = 8$

y el argumento es: $α = \arctan (\frac{4 \sqrt{3}}{4}) = \arctan (\sqrt{3}) = 60^{\circ}$

porqué tanto la parte real como la imaginaria son positivas y por lo tanto el complejo vive en el primer cuadrante.

De manera que para representarlo en forma polar este complejo es $z = | z |_{α} = 8_{60^{\circ}}$

Esta manera de trabajar nos permite pasar de un número complejo expresado en forma binómica a un número complejo expresado en forma polar.