Ja sabem treballar amb la forma binòmica dels nombres complexos i sabem els passos a seguir per representar-los en el pla complex.
El que fèiem era adjudicar un vector a cada nombre complex, que determinàvem segons les seves parts real i imaginària. Així doncs, en el fons estàvem representant vectors en el pla.
Però els vectors en el pla poden ser entesos també com una longitud i un angle que els separa de l'eix horitzontal. Per això, els nombres imaginaris també es poden entendre com una longitud (que serà el mòdul) i un angle. Vegem com es construeix.
Per a representar un nombre complex $$z$$ en forma polar s'han de considerar el mòdul i l'argument d'aquest. El mòdul es refereix a la longitud del vector que el representa en el pla i l'argument es refereix a l'angle que forma amb l'eix horitzontal.
És a dir, gràficament seria:
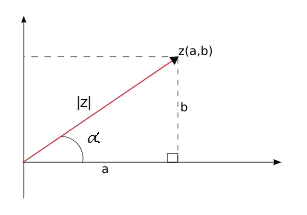
Així, representarem un nombre complex mitjançant un mòdul i un argument que escriurem de la forma $$z=|z|_{\alpha}$$ on:
- a $$|z|$$ se l'anomena mòdul i és l'arrel quadrada de la suma dels quadrats de la component real i la component imaginària. Se sol escriure $$|z|$$ o $$r$$ i es pot pensar com la distància des de l'origen fins al nombre complex $$z$$ si el tenim representat en el pla complex. Així doncs, es té: $$$ |z|=|a+bi|=\sqrt{a^2+b^2}$$$
- a $$\alpha$$ se l'anomena l'argument del nombre complex $$z$$ i és l'angle que forma el nombre complex $$z$$ amb l'eix real (en sentit positiu) si ho tenim representat en el pla complex. Així doncs, es té: $$$\alpha=\arctan(\dfrac{b}{a})$$$
Es té llavors que l'argument d'un nombre complex no és únic, ja que l'expressió $$\alpha=\arctan(\frac{b}{a})$$ no determina unívocament l'argument d'un nombre, ja que hi ha infinits angles que compleixen la igualtat.
Ara bé, si restringim el valor de $$\alpha$$ per $$0\leqslant\alpha< 2\pi$$, només hi haurà dos angles que difereixen en $$\pi$$ i tenen la mateixa tangent. Per saber quin d'ells és l'argument, tindrem en compte els signes de $$a$$ i $$b$$, d'aquesta manera aconseguirem saber en quin quadrant està situat el vector del nombre complex i ens donarà l'angle que busquem.
- Si la part real i la imaginària són positives, el complex es troba al primer quadrant.
Per exemple $$5+9i$$.
- Si la part real és negativa i la imaginària és positiva, el complex es troba en el segon quadrant.
Per exemple $$-5+9i$$.
- Si la part real i la imaginària són negatives, el complex es troba al tercer quadrant.
Per exemple $$-5-9i$$.
- Si la part real és positiva i la imaginària és negativa, el complex es troba en el quart quadrant.
Per exemple $$5-9i$$.
Calculem el mòdul i argument del nombre $$z=4+4\sqrt{3}i$$.
El complex $$4+4\sqrt{3}i$$ té per mòdul: $$$|4+4\sqrt{3}i|=\sqrt{4^2+(4\sqrt{3})^2}=\sqrt{16+16\cdot3}=\sqrt{16+48}= \sqrt{64}=8$$$
I l'argument és: $$$\alpha=\arctan\Big(\dfrac{4\sqrt{3}}{4}\Big) =\arctan(\sqrt{3})=60^{\circ}$$$
perquè tant la part real com la imaginària són positives i per tant el complex viu al primer quadrant.
De manera que aquest complex en forma polar és: $$$ z=|z|_{\alpha}=8_{60^{\circ}}$$$
Aquesta manera de treballar ens permet passar d'un nombre complex expressat en forma binòmica a un nombre complex expressat en forma polar.