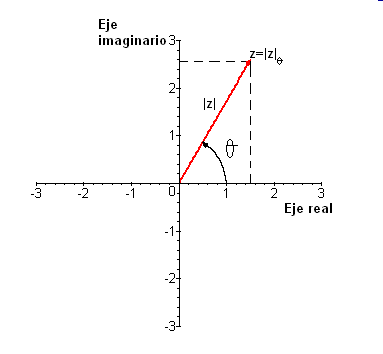Dado un número complejo $$z$$ se pueden considerar sus dos maneras de representación que se saben hasta ahora. Así pues, se puede tener:
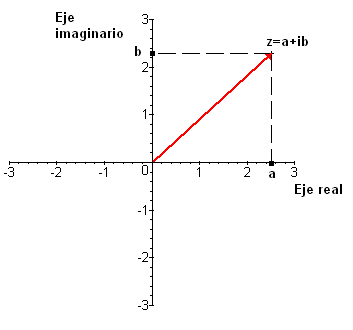
- Forma binómica: dado un complejo en forma binómica $$z=a+bi$$ también se le puede identificar con un par ordenado al que llamaremos coordenadas cartesianas. Este par es
$$(a, b)$$ y nos permite dibujar $$z$$ en el plano complejo. El procedimiento es:
- Dibujar en el eje OX (eje real) la primera componente del par ordenado. Es decir la parte real de $$z$$.
- Dibujar en el eje OY (eje imaginario) la segunda componente del par ordenado. Es decir la parte imaginaria de $$z$$.
- Marcar el punto donde se encuentran las rectas paralelas a los ejes OX y OY que pasan por $$a$$ y $$b$$.
- Unir el origen del plano complejo con el punto marcado. Ése es el número complejo $$z$$.
-
Forma polar: El número complejo dado en forma polar $$z=|z|_{\alpha}$$ se puede identificar con el par $$(|z|,\alpha)$$ que serán sus coordenadas polares que permitirán dibujar $$z$$ en el plano complejo. El procedimento es:
- Dibujar un ángulo $$\alpha$$ que salga del origen del plano complejo.
- Coger el módulo de $$z$$, es decir $$|z|$$, y ponerlo encima del ángulo. Esa longitud es la que nos determina el número $$z$$ en el plano complejo.