Sum and subtract of vectors

Sum of two free vectors $\vec{u}$ and $\vec{v}$ The sum of these two free vectors is another free vector $\vec{u} + \vec{v}$ , which is obtained as follows:

We take the second of the two vectors and we put it at the ending point of the first one. That is, the origin of the second vector is the same as the end of the first vector. The vector sum will be the one that has the origin of the first vector $\vec{u}$ and the end of the second vector $\vec{v}$ .

Another way of adding two free vectors is by using the rule of the parallelogram: We take the two vectors sharing the same origin. We then take a paralel line through both ending points so that we obtain a parallelogram. The diagonal of this parallelogram will then coincide with the sum of the two vectors.

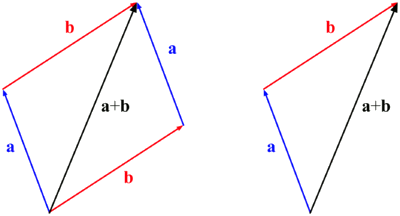
imagen

To add two vectors, it is enough to add its respective components, that is, if $\vec{u} = (x_{1}, y_{1})$ and $\vec{v} = (x_{2}, y_{2})$ : $\vec{u} + \vec{v} = (x_{1} + x_{2}, y_{1} + y_{2})$

Example

If $\vec{u} = (- 5, 3)$ and $\vec{v} = (1, 1)$ , then: $\vec{u} + \vec{v} = (- 5 + 1, 3 + 1) = (- 4, 4)$

To subtract two free vectors $\vec{u} = (x_{1}, y_{1})$ and $\vec{v} = (x_{2}, y_{2})$ , that is if we want to find $\vec{u} - \vec{v}$ , we add the $\vec{u}$ with the inverse of $\vec{v} = (x_{2}, y_{2})$ , $- \vec{v}$ .

Example

If $\vec{u} = (2, 6)$ and $\vec{v} = (3, 2)$ , the subtraction $\vec{u} - \vec{v}$ will be the sum of $\vec{u}$ and $- \vec{v} = (- 3, - 2)$ (l'oposat de $\vec{v}$ ), so that: $\vec{u} - \vec{v} = (2 + (- 3), 6 + (- 2)) = (- 1, 4)$

Properties of the sum:

Associative: $\vec{u} + (\vec{v} + \vec{w}) = (\vec{u} + \vec{v}) + \vec{w}$ .
Commutative: $\vec{u} + \vec{v} = \vec{v} + \vec{u}$ .
Identity element: $\vec{u} + \vec{0} = \vec{0} + \vec{u} = \vec{u}$ .
(Inverse) symmetrical element: $\vec{u} + (- \vec{u}) = (- \vec{u}) + \vec{u} = \vec{0}$ .