Suma de dos vectores libres $$\vec{u}$$ y $$\vec{v}$$. La suma de estos dos vectores libres es otro vector libre $$\vec{u}+\vec{v}$$, que se obtiene de la siguiente forma:
Se escogen como representantes dos vectores tales que el extremo de uno coincida con el origen del otro vector. El vector suma tendrá como origen el origen de $$\vec{u}$$ y como extremo el extremo de $$\vec{v}$$.
Otra manera de sumar dos vectores libres es mediante la regla del paralelogramo: Se toman como representantes dos vectores con el origen en común, se trazan rectas paralelas a los vectores obteniéndose un paralelogramo cuya diagonal coincide con la suma de los vectores.
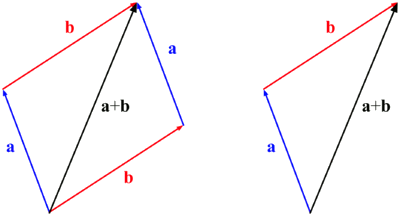
Para sumar dos vectores, basta sumar sus respectivas componentes, si $$\vec{u}=(x_1,y_1)$$ y $$\vec{v}=(x_2,y_2)$$: $$$\vec{u}+\vec{v}=(x_1+x_2,y_1+y_2)$$$
Si $$\vec{u}=(-5,3)$$ y $$\vec{v}=(1,1)$$, entonces: $$$\vec{u}+\vec{v}=(-5+1,3+1)=(-4,4)$$$
Para restar dos vectores libres $$\vec{u}=(x_1,y_1)$$ y $$\vec{v}=(x_2,y_2)$$, es decir, $$\vec{u}-\vec{v}$$, se suma $$\vec{u}$$ con el opuesto de $$\vec{v}=(x_2,y_2)$$, que seria $$-\vec{v}$$.
Si $$\vec{u}=(2,6)$$ y $$\vec{v}=(3,2)$$, la resta $$\vec{u}-\vec{v}$$ serà la suma de $$\vec{u}$$ y $$-\vec{v}=(-3,-2)$$ (l'oposat de $$\vec{v}$$), de manera que: $$$ \vec{u}-\vec{v}=(2+(-3),6+(-2))=(-1,4)$$$
Propiedades de la suma:
- Asociativa: $$\vec{u}+(\vec{v}+\vec{w})=(\vec{u}+\vec{v})+\vec{w}$$.
- Commutativa: $$\vec{u}+\vec{v}=\vec{v}+\vec{u}$$.
- Elemento neutro: $$\vec{u}+\vec{0}=\vec{0}+\vec{u}=\vec{u}$$.
- Elemento simétrico (opuesto): $$\vec{u}+(-\vec{u})=(-\vec{u})+\vec{u}=\vec{0}$$.