La suma de dos vectors lliures $$\vec{u}$$ i $$\vec{v}$$ és un altre vector lliure $$\vec{u}+\vec{v}$$, que s'obté de la següent manera:
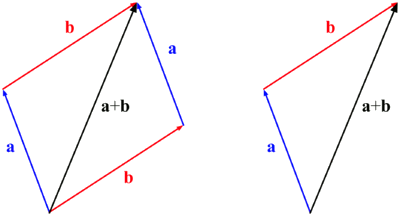
Es trien com a representants dos vectors tals que l'extrem d'un coincideixi amb l'origen de l'altre vector. El vector suma tindrà com a origen l'origen de $$\vec{u}$$ i com a extrem, l'extrem de $$\vec{v}$$.
Una altra manera de sumar dos vectors lliures és mitjançant la regla del paral·lelogram: Es prenen com a representants dos vectors amb l'origen en comú, es tracen rectes paral·leles als vectors obtenint-se un paral·lelogram la diagonal del qual coincideix amb la suma dels vectors.
Per sumar dos vectors, només cal sumar els seus respectives components, si $$\vec{u}=(x_1,y_1)$$ i $$\vec{v}=(x_2,y_2)$$: $$$\vec{u}+\vec{v}=(x_1+x_2,y_1+y_2)$$$
Si $$\vec{u}=(-5,3)$$ i $$\vec{v}=(1,1)$$, aleshores: $$$\vec{u}+\vec{v}=(-5+1,3+1)=(-4,4)$$$
Per restar dos vectors lliures $$\vec{u}=(x_1,y_1)$$ i $$\vec{v}=(x_2,y_2)$$, és a dir, $$\vec{u}-\vec{v}$$, se suma $$\vec{u}$$ amb l'oposat de $$\vec{v}=(x_2,y_2)$$, que seria $$-\vec{v}$$.
Si $$\vec{u}=(2,6)$$ i $$\vec{v}=(3,2)$$, la resta $$\vec{u}-\vec{v}$$ serà la suma de $$\vec{u}$$ i $$-\vec{v}=(-3,-2)$$ (l'oposat de $$\vec{v}$$), de manera que: $$$ \vec{u}-\vec{v}=(2+(-3),6+(-2))=(-1,4)$$$
Propietats de la suma:
- Associativa: $$\vec{u}+(\vec{v}+\vec{w})=(\vec{u}+\vec{v})+\vec{w}$$.
- Commutativa: $$\vec{u}+\vec{v}=\vec{v}+\vec{u}$$.
- Element neutre: $$\vec{u}+\vec{0}=\vec{0}+\vec{u}=\vec{u}$$.
- Element simètric (oposat): $$\vec{u}+(-\vec{u})=(-\vec{u})+\vec{u}=\vec{0}$$.
