The objective is to add the first $$n$$ terms of a geometric progression.
We take the geometric progression of the first term $$a_1=3$$ and ratio $$r=2$$. We denote $$S_n$$ the sum of the first $$n$$ terms, and we are going to calculate the value of $$S_n$$ for $$n=1,2,3,\ldots,10$$.
The first ten terms are:
$$3,6,12,24,48,96,192,384,768,1.536$$
And the values of the sums:
$$S_1=3$$
$$S_2=3+6=9$$
$$S_3=3+6+12=21$$
$$S_4=3+6+12+24=45$$
$$S_5=3+6+12+24+48=93$$
$$S_6=3+6+12+24+48+96=189$$
$$S_7=3+6+12+24+48+96+192=381$$
$$S_8=3+6+12+24+48+96+192+284=765$$
$$S_9=3+6+12+24+48+96+192+284+768=1.533$$
$$S_{10}=3+6+12+24+48+96+192+284+768+1.536=3.069$$
As expected (we are adding positive terms), we obtain an increasing result. Then we ask ourselves: can it become infinitely big or will the numbers level off at some point?
Let's consider now the progression of the first term $$a_1=7$$, and ratio $$r=\dfrac{1}{3}$$.
We write its first ten terms:
$$7, \dfrac{7}{3}, \dfrac{7}{9}, \dfrac{7}{27}, \dfrac{7}{81}, \dfrac{7}{243}, \dfrac{7}{729}, \dfrac{7}{2.187}, \dfrac{7}{6.561}, \dfrac{7}{19.683}$$
And we calculate the sums:
$$S_1=7$$
$$S_2=7 + \dfrac{7}{3}=9,3$$
$$S_3=7 + \dfrac{7}{3}+ \dfrac{7}{9}=10,1$$
$$S_4=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}=10,37037$$
$$S_5=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}=10,45679012$$
$$S_6=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}=10,4855967$$
$$S_7=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}+\dfrac{7}{729}=10,4951989$$
$$S_8=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}+\dfrac{7}{729}+\dfrac{7}{2.187}=10,498699639$$
$$S_9=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}+\dfrac{7}{729}+\dfrac{7}{2.187}+\dfrac{7}{6.561}=10,49946654$$
$$S_{10}=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}+\dfrac{7}{729}+\dfrac{7}{2.187}+$$
$$+\dfrac{7}{6.561}+\dfrac{7}{19.683}=10,49982218$$
Note that the sums of the second progression are also increasing, but not rising as fast as in the previous example. In fact, it seems to be a manageable growth: for the obtained results, the amounts are getting closer to $$10,5$$. Will it exceed this value at any point or, if not, will it become an upper bound of the values $$S_n$$? And, in this case, will we obtain an approximation to $$10,5$$ as good as we want it if we add enough terms?
Let's consider now a theoretical case:
If $$a_1, a_2, \ldots ,a_n$$ are the first $$n$$ terms of a geometric progression of ratio $$r$$. Then,
$$$S_n=a_1+a_2+\ldots +a_n= a_1+a_1\cdot r + \ldots + a_1 \cdot r^{n-1}$$$
Multiplying both members of the equality by $$r$$, the following is obtained:
$$$r\cdot S_n=a_1\cdot r+a_1\cdot r^2 + \ldots + a_1 \cdot r^{n}$$$
By reducing, member by member, these two equalities, we obtain:
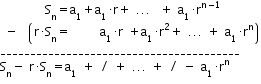
Namely, we have:
$$S_n - r\cdot S_n = a_1 - a_1 \cdot r^n$$
So:
$$$S_n(1-r)=a_1(1-r^n) \Rightarrow S_n=\dfrac{a_1(1-r^n)}{1-r}$$$
Remembering the previous examples,
If $$a_n=3\cdot 2^{n-1}$$, then, $$$S_n=\dfrac{a_1(1-r^n)}{1-r}=\dfrac{3(1-2^2)}{1-2}=3(2^n-1)$$$
In such a way that, if we allow $$n$$ to grow indefinitely, $$S_n$$ will not stop growing, since $$2^n$$ can grow indefinitely if we choose an $$n$$ big enough.
If in this expression we substitute $$n$$ by any value, for example $$10$$, we will obtain the result of adding the first $$10$$ terms.
On the other hand, if $$b_n=\dfrac{7}{3^{n-1}}$$, then, $$$S_n=\dfrac{7\Big(1-\dfrac{1}{3^n}\Big)}{1-\dfrac{1}{3}}=\dfrac{21}{2}\Big[1-\Big(\dfrac{1}{3}\Big)^n\Big]$$$
In this case, the base of the nth power is less than the unit, which means that as the value of $$n$$ increases, $$\Big(\dfrac{1}{3}\Big)^n$$ decreases. Because of this, the value of $$S_n$$ stabilizes if we choose $$n$$ to be big enough.