El objetivo es sumar los primeros $$n$$ términos de una progresión geométrica.
Tomamos la progresión geométrica de primer término $$a_1=3$$ y razón $$r=2$$. Denotamos $$S_n$$ la suma de los primeros $$n$$ términos, y calculamos el valor de $$S_n$$ para $$n=1,2,3,\ldots,10$$.
Los primeros diez términos son:
$$3,6,12,24,48,96,192,384,768,1.536$$
Y los valores de las sumas:
$$S_1=3$$
$$S_2=3+6=9$$
$$S_3=3+6+12=21$$
$$S_4=3+6+12+24=45$$
$$S_5=3+6+12+24+48=93$$
$$S_6=3+6+12+24+48+96=189$$
$$S_7=3+6+12+24+48+96+192=381$$
$$S_8=3+6+12+24+48+96+192+284=765$$
$$S_9=3+6+12+24+48+96+192+284+768=1.533$$
$$S_{10}=3+6+12+24+48+96+192+284+768+1.536=3.069$$
Tal como era de esperar (estamos sumando términos positivos), obtenemos un resultado cada vez mayor. Luego nos preguntamos: pueden llegar a ser tan grandes como queramos, o por contra, llegará un momento en que se estacionarán?
Consideremos ahora la progresión de primer término $$a_1=7$$, y razón $$r=\dfrac{1}{3}$$.
Escribimos los diez primeros términos:
$$7, \dfrac{7}{3}, \dfrac{7}{9}, \dfrac{7}{27}, \dfrac{7}{81}, \dfrac{7}{243}, \dfrac{7}{729}, \dfrac{7}{2.187}, \dfrac{7}{6.561}, \dfrac{7}{19.683}$$
Y calculamos las sumas:
$$S_1=7$$
$$S_2=7 + \dfrac{7}{3}=9,3$$
$$S_3=7 + \dfrac{7}{3}+ \dfrac{7}{9}=10,1$$
$$S_4=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}=10,37037$$
$$S_5=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}=10,45679012$$
$$S_6=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}=10,4855967$$
$$S_7=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}+\dfrac{7}{729}=10,4951989$$
$$S_8=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}+\dfrac{7}{729}+\dfrac{7}{2.187}=10,498699639$$
$$S_9=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}+\dfrac{7}{729}+\dfrac{7}{2.187}+\dfrac{7}{6.561}=10,49946654$$
$$S_{10}=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}+\dfrac{7}{729}+\dfrac{7}{2.187}+$$
$$+\dfrac{7}{6.561}+\dfrac{7}{19.683}=10,49982218$$
Observemos que las sumas de esta segunda progresión son también cada vez mayores, pero su crecimiento no es tan rápido como el anterior ejemplo; de hecho, parece un crecimiento controlable: para los resultados obtenidos, las sumas se acercan cada vez más a $$10,5$$. Llegará en algún momento a superar este valor, o por lo contrario constituirá una cota superior a los valores $$S_n$$? Y en este caso, obtendremos una aproximación de $$10,5$$ tan buena como queramos si sumamos suficientes términos?
Consideremos ahora un caso teórico:
Si $$a_1, a_2, \ldots ,a_n$$ son los primeros $$n$$ términos de una progresión geométrica de razón $$r$$. Entonces,
$$$S_n=a_1+a_2+\ldots +a_n= a_1+a_1\cdot r + \ldots + a_1 \cdot r^{n-1}$$$
Multiplicando los dos miembros de la igualdad por $$r$$, se obtiene:
$$$r\cdot S_n=a_1\cdot r+a_1\cdot r^2 + \ldots + a_1 \cdot r^{n}$$$
Restando miembro a miembro estas dos igualdades, obtenemos:
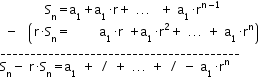
Es decir, nos queda que:
$$S_n - r\cdot S_n = a_1 - a_1 \cdot r^n$$
Por lo que:
$$$S_n(1-r)=a_1(1-r^n) \Rightarrow S_n=\dfrac{a_1(1-r^n)}{1-r}$$$
Recordando los ejemplos anteriores,
Si $$a_n=3\cdot 2^{n-1}$$, entonces, $$$S_n=\dfrac{a_1(1-r^n)}{1-r}=\dfrac{3(1-2^2)}{1-2}=3(2^n-1)$$$
De tal forma que, si hacemos crecer $$n$$ indefinidamente, $$S_n$$ no dejará de crecer, ya que $$2^n$$ puede crecer indefinidamente, si escogemos una $$n$$ suficientemente grande.
Si en esta expresión sustituimos $$n$$ por cualquier valor, por ejemplo por $$10$$, encontraremos el resultado de sumar los primeros $$10$$ términos.
Por otra parte, si $$b_n=\dfrac{7}{3^{n-1}}$$, entonces, $$$S_n=\dfrac{7\Big(1-\dfrac{1}{3^n}\Big)}{1-\dfrac{1}{3}}=\dfrac{21}{2}\Big[1-\Big(\dfrac{1}{3}\Big)^n\Big]$$$
En esta ocasión, la base de la potencia n-ésima es menor que la unidad, lo que significa que aumentado el valor de $$n$$, $$\Big(\dfrac{1}{3}\Big)^n$$ disminuye. Debido a esto, el valor de $$S_n$$ se estaciona para $$n$$ suficientemente grandes.