L'objectiu és sumar els primers $$n$$ termes d'una progressió geomètrica.
Prenem la progressió geomètrica de primer terme $$a_1=3$$ i raó $$r=2$$. Denotem $$S_n$$ la suma dels primers $$n$$ termes, i calculem el valor de $$S_n$$ per a $$n=1,2,3,\ldots,10$$.
Els primers deu termes són:
$$3,6,12,24,48,96,192,384,768,1.536$$
I els valors de les sumes:
$$S_1=3$$
$$S_2=3+6=9$$
$$S_3=3+6+12=21$$
$$S_4=3+6+12+24=45$$
$$S_5=3+6+12+24+48=93$$
$$S_6=3+6+12+24+48+96=189$$
$$S_7=3+6+12+24+48+96+192=381$$
$$S_8=3+6+12+24+48+96+192+284=765$$
$$S_9=3+6+12+24+48+96+192+284+768=1.533$$
$$S_{10}=3+6+12+24+48+96+192+284+768+1.536=3.069$$
Tal com era d'esperar (estem sumant termes positius), obtenim un resultat cada vegada més gran. Després ens preguntem: poden arribar a ser tan grans com vulguem, o per contra, arribarà un moment en que s'estacionaran?
Considerem ara la progressió de primer terme $$a_1=7$$, i raó $$r=\dfrac{1}{3}$$.
Escrivim els primers deu termes:
$$7, \dfrac{7}{3}, \dfrac{7}{9}, \dfrac{7}{27}, \dfrac{7}{81}, \dfrac{7}{243}, \dfrac{7}{729}, \dfrac{7}{2.187}, \dfrac{7}{6.561}, \dfrac{7}{19.683}$$
I calculem les sumes:
$$S_1=7$$
$$S_2=7 + \dfrac{7}{3}=9,3$$
$$S_3=7 + \dfrac{7}{3}+ \dfrac{7}{9}=10,1$$
$$S_4=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}=10,37037$$
$$S_5=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}=10,45679012$$
$$S_6=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}=10,4855967$$
$$S_7=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}+\dfrac{7}{729}=10,4951989$$
$$S_8=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}+\dfrac{7}{729}+\dfrac{7}{2.187}=10,498699639$$
$$S_9=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}+\dfrac{7}{729}+\dfrac{7}{2.187}+\dfrac{7}{6.561}=10,49946654$$
$$S_{10}=7+\dfrac{7}{3}+\dfrac{7}{9}+\dfrac{7}{27}+\dfrac{7}{81}+\dfrac{7}{243}+\dfrac{7}{729}+\dfrac{7}{2.187}+$$
$$+\dfrac{7}{6.561}+\dfrac{7}{19.683}=10,49982218$$
Observem que les sumes d'aquesta segona progressió són també cada vegada més grans, però el seu creixement no és tan ràpid com l'anterior exemple, de fet, sembla un creixement controlable: per als resultats obtinguts, les sumes s'acosten cada vegada més a $$10,5$$. Arribarà en algun moment a superar aquest valor, o pel contrari constituirà una cota superior als valors $$S_n$$? I en aquest cas, obtindrem una aproximació de $$10,5$$ tan bona com vulguem si sumem suficients termes?
Considerem ara un cas teòric:
Si $$a_1, a_2, \ldots ,a_n$$ són els primers $$n$$ termes d'una progressió geomètrica de raó $$r$$. Llavors,
$$$S_n=a_1+a_2+\ldots +a_n= a_1+a_1\cdot r + \ldots + a_1 \cdot r^{n-1}$$$
Multiplicant els dos membres de la igualtat per $$r$$, s'obté:
$$$r\cdot S_n=a_1\cdot r+a_1\cdot r^2 + \ldots + a_1 \cdot r^{n}$$$
Restant membre a membre aquestes dues igualtats, obtenim:
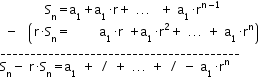
És a dir, ens queda que:
$$S_n - r\cdot S_n = a_1 - a_1 \cdot r^n$$
Pel que:
$$$S_n(1-r)=a_1(1-r^n) \Rightarrow S_n=\dfrac{a_1(1-r^n)}{1-r}$$$
Recordant els exemples anteriors,
Si $$a_n=3\cdot 2^{n-1}$$, llavors, $$$S_n=\dfrac{a_1(1-r^n)}{1-r}=\dfrac{3(1-2^2)}{1-2}=3(2^n-1)$$$
De tal manera que, si fem créixer $$n$$ indefinidament, $$S_n$$ no deixarà de créixer, ja que $$2^n$$ pot créixer indefinidament, si escollim una $$n$$ suficientment gran.
Si en aquesta expressió substituim $$n$$ per qualsevol valor, per eexemple per $$10$$, trobarem el resultat de sumar els primers $$10$$ termes.
Per altra banda, si $$b_n=\dfrac{7}{3^{n-1}}$$, llavors, $$$S_n=\dfrac{7\Big(1-\dfrac{1}{3^n}\Big)}{1-\dfrac{1}{3}}=\dfrac{21}{2}\Big[1-\Big(\dfrac{1}{3}\Big)^n\Big]$$$
En aquesta ocasió, la base de la potència n-èsima és menor que la unitat, el que significa que augmentat el valor de $$n$$, $$\Big(\dfrac{1}{3}\Big)^n$$ disminueix.A causa d'això, el valor de $$S_n$$ s'estaciona per a $$n$$ suficientment grans.
