The frustum of pyramid: Surface area and volume

It is the resultant polyhedron after having made a parallel cut to the basis of a pyramid. The mentioned cut will be named a minor base.

Lateral faces will have now the shape of isosceles trapeze.
The height will be the distance between basis.

The following figure is an example of a frustum of pyramid with pentagonal bases.

imagen

Example

Calculate the area of a frustum of pyramid of basis squared with: $A_{b a s i s} = 16 m^{2} A_{m i n o r b a s i s} = 9 m^{2} h e i g h t = 3$ To find the area of the trapeze sides, it is necessary to calculate the value of $A p$ , the apothem of the frustum of pyramid, or height of the trapeze:

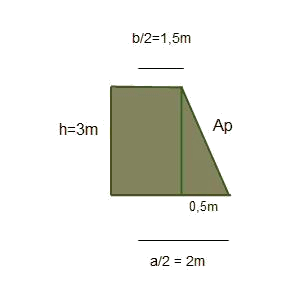
imagen

$a$ being the side of the basis and $b$ the side of the minor basis. Analyzing the triangle that remains, of basis $0, 5 m$ : $A p^{2} = 0, 5^{2} + 3^{2} A p = 3, 04 m$

Now that we already have the apothem, we calcule the area of the side, $A_{l a t e r a l} = (P e r i m e t r e_{b a s i s} + P e r i m e t r e_{m i n o r b a s i s}) \frac{A p}{2} A_{l a t e r a l} = (16 + 12) \cdot \frac{3, 04}{2} = 42, 56 m^{2}$ And the entire area will be: $A_{t o t a l} = A_{l a t e r a l s} + A_{b a s i s} + A_{m i n o r b a s i s} A_{t o t a l} = 42, 56 + 9 + 16 = 67, 56 m^{2}$

To calculate the volume of the pyramidal frustum we will use the following expression ( $h$ is the height, $A$ is the area of the basis and $A^{'}$ the area of the minor basis) $V = \frac{h}{3} (A + A^{'} + \sqrt{A \cdot A^{'}})$

In the previous example the mentioned volume has a value of $V = 55, 5 m^{3}$ .