El tronc de piràmide: Àrea i volum

És el políedre resultant de realitzar un tall paral.lel a la base d'una piràmide. Aquest tall serà anomenat base menor.

Les cares laterals tindran ara forma de trapezi isòsceles.
L'alçada serà la distància entre bases.

La següent figura mostra un tronc de piràmide amb base pentagonal.

imagen

Exemple

Calcular l'àrea d'un tronc de piràmide de bases quadrades amb: $A_{b a s e} = 16 m^{2} A_{b a s e m e n o r} = 9 m^{2} a l t u r a = 3 m$ Per trobar l'àrea dels trapezis laterals, cal calcular el valor de $A p$ , l' apotema del tronc de piràmide, o alçada del trapezi:

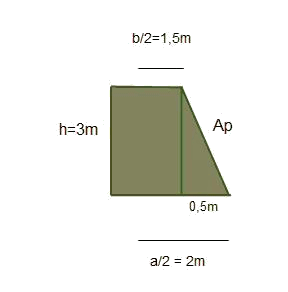
imagen

sent $a$ el costat de la base i $b$ el costat de la base menor. Analitzant el triangle que queda té de base $0, 5 m$ : $A p^{2} = 0, 5^{2} + 3^{2} A p = 3, 04 m$

Tenint ja l'apotema, es calcula l'àrea lateral, $A_{l a t e r a l} = (P e r í m e t r e_{b a s e} + P e r í m e t r e_{b a s e m e n o r}) \frac{A p}{2} A_{l a t e r a l} = (16 + 12) \cdot \frac{3, 04}{2} = 42, 56 m^{2}$ I l'àrea total serà: $A_{t o t a l} = A_{l a t e r a l s} + A_{b a s e} + A_{b a s e m e n o r} A_{t o t a l} = 42, 56 + 9 + 16 = 67, 56 m^{2}$

Per calcular el volum del tronc piramidal s'utilitzarà la següent expressió (on $h$ és l'altura, $A$ és l'àrea de la base i $A^{'}$ l'àrea de la base menor) $V = \frac{h}{3} (A + A^{'} + \sqrt{A \cdot A^{'}})$

En l'exemple anterior aquest volum té un valor de $V = 55, 5 m^{3}$ .