Es el poliedro resultante de realizar un corte paralelo a la base de una pirámide. Dicho corte será denominado base menor.
-
Las caras laterales tendrán ahora forma de trapecio isósceles.
- La altura será la distancia entre bases.
La siguiente figura muestra un tronco de pirámide con base pentagonal.
Calcular el área de un tronco de pirámide de bases cuadradas con: $$$A_{base}=16 \ m^2 \\ A_{base \ menor}= 9 \ m^2 \\ altura = 3 \ m$$$ Para encontrar el área de los trapecios laterales, es necesario calcular el valor de $$Ap$$, el apotema del tronco de pirámide, o altura del trapecio:
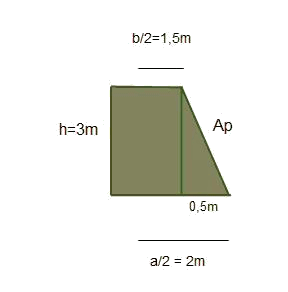
siendo $$a$$ el lado de la base y $$b$$ el lado de la base menor. Analizando el triángulo que queda tiene de base $$0,5 \ m$$: $$$Ap^2=0,5^2+3^2 \\ Ap=3,04 \ m$$$
Teniendo ya el apotema, se calcula el área lateral, $$$A_{lateral}=\Big(Perímetro _{base}+Perímetro_{base \ menor}\Big) \dfrac{Ap}{2} \\ A_{lateral}=(16+12) \cdot \dfrac{3,04}{2}=42,56 \ m^2$$$ Y el área total será: $$$A_{total}=A_{laterales}+A_{base}+A_{base \ menor} \\ A_{total}=42,56+9+16=67,56 \ m^2$$$
Para calcular el volumen del tronco piramidal se utilizará la siguiente expresión ($$h$$ es la altura, $$A$$ es el área de la base y $$A'$$ el área de la base menor) $$$V=\dfrac{h}{3}(A+A'+\sqrt{A\cdot A'})$$$
Dicho volumen tiene un valor de $$V=55,5 m^3$$.

