Trigonometric identities of other angles

Supplementary angles

Two angles are said to be supplementary if they add up to $180^{\circ}$ .

Example

For example, an angle of $140^{\circ}$ and one of $40^{\circ}$ are supplementary since: $140^{\circ} + 40^{\circ} = 180^{\circ}$

imagen

The sine, cosine and tangent of the supplementary angles have a certain relation. That is, if $α$ and $β$ are two supplementary angles then we have:

$\sin (α) = \sin (β)$
$\cos (α) = - \cos (β)$
$\tan (α) = - \tan (β)$

So we have that their sines are equal, and their cosine and their tangent are equal with opposed signs.

Example

In the previous example, then, we have:

$\sin (40^{\circ}) = \sin (140^{\circ})$
$\cos (40^{\circ}) = - \cos (140^{\circ})$
$\tan (40^{\circ}) = - \tan (140^{\circ})$

Angles that differ in $180^{\circ}$

Two angles $α$ and $β$ are said to differ in $180^{\circ}$ if $α - β = 180^{\circ}$ .

Example

For example an angle of $240^{\circ}$ and one of $60^{\circ}$ differ in $180^{\circ}$ , since: $240^{\circ} - 60^{\circ} = 180^{\circ}$

imagen

The sine, cosine and tangent of two angles that differ in $180^{\circ}$ are also related. If $α$ and $β$ differ in $180^{\circ}$ , we have:

$\sin (α) = - \sin (β)$
$\cos (α) = - \cos (β)$
$\tan (α) = \tan (β)$

That is, the sine and the cosine have equal values but differ in their signs, while the tangent is equal.

Example

In the previous example, therefore, we have:

$\sin (240^{\circ}) = - \sin (60^{\circ})$
$\cos (240^{\circ}) = - \cos (60^{\circ})$
$\tan (240^{\circ}) = \tan (60^{\circ})$

Opposite angles

Two angles are said to be opposite angles if they add up to $360^{\circ}$ . That is, $α$ and $β$ are opposite angles if $α + β = 360^{\circ}$ .

Example

For example, an angle of $330^{\circ}$ and one of $30^{\circ}$ are opposite angles, since $330^{\circ} + 30^{\circ} = 360^{\circ}$

imagen

The sines, cosines and tangent of opposite angles are related in a similar way as the one we saw with the supplementary angles or those which differ in $180^{\circ}$ . That is, if $α$ and $β$ are opposite angles we have:

$\sin (α) = - \sin (β)$
$\cos (α) = \cos (β)$
$\tan (α) = - \tan (β)$

That is, the sine and the tangent are equal but with different signs, and the cosine is exactly the same.

Example

In the previous example we have:

$\sin (330^{\circ}) = - \sin (30^{\circ})$
$\cos (330^{\circ}) = \cos (30^{\circ})$
$\tan (330^{\circ}) = - \tan (30^{\circ})$

Negative angles

An angle is negative if it goes clockwise, and it is symbolized by a minus sign.

Example

For example, if there is an angle of $30^{\circ}$ , but instead of going up it goes down, or clockwise, it is said that the angle is of $- 30^{\circ}$ .

The following illustration shows the negative angle $- 30^{\circ}$ :

imagen

If $α$ is an angle, then we have the following identities:

$\sin (- α) = - \sin (α)$
$\cos (- α) = \cos (α)$
$\tan (- α) = - \tan (α)$

In short, the sine and the tangent of $α$ and $- α$ are the same but with different signs, and the cosine is exactly the same.

Example

In the previous example we have:

$\sin (- 30^{\circ}) = - \sin (30^{\circ})$
$\cos (- 30^{\circ}) = \cos (30^{\circ})$
$\tan (- 30^{\circ}) = - \tan (30^{\circ})$

Angles greater than $360^{\circ}$

To find the sine, the cosine and the tangent of an angle greater than $360^{\circ}$ , we have to do the following:

The integer division of the given angle over $360$ . For example, if the angle is $780^{\circ}$ , then:
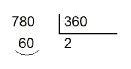
We then take the residual. In the previous example it is $60^{\circ}$ .
The sine, the cosine and the tangent of the given angle are that of the residual that has been obtained.

Example

Going back to the previous example, we have:

$\sin (780^{\circ}) = \sin (660^{\circ})$
$\cos (780^{\circ}) = \cos (60^{\circ})$
$\tan (780^{\circ}) = \tan (60^{\circ})$

Angles that differ in $90^{\circ}$

Two angles differ in $90^{\circ}$ if the result of subtracting them is $90^{\circ}$ .

Example

For example, an angle of $160^{\circ}$ and one of $70^{\circ}$ , ja que: $160^{\circ} - 70^{\circ} = 90^{\circ}$ . The following illustration shows it more clearly:

imagen

If it is true that two angles, $α$ and $β$ , differ in $90^{\circ}$ (that is to say, if $α - β = 90^{\circ}$ ) then:

$\sin (α) = \cos (β)$
$\cos (α) = - \sin (β)$
$\tan (α) = - \cot (β)$

Example

In the previous example we have that:

$\sin (160^{\circ}) = \cos (70^{\circ})$
$\cos (160^{\circ}) = - \sin (70^{\circ})$
$\tan (160^{\circ}) = - \cot (70^{\circ})$

Angles that add up to $270^{\circ}$

Two angles $α$ and $β$ add up $270^{\circ}$ if $α + β = 270^{\circ}$ .

Example

For example, an angle of $70^{\circ}$ and one of $200^{\circ}$ , since $70^{\circ} + 200^{\circ} = 270^{\circ}$ .

In this case, $α$ and $β$ satisfy the following identities:

$\sin (α) = - \cos (β)$
$\cos (α) = - \sin (β)$
$\tan (α) = \cot (β)$

Example

In the previous example, we have:

$\sin (70^{\circ}) = - \cos (200^{\circ})$
$\cos (70^{\circ}) = - \sin (200^{\circ})$
$\tan (70^{\circ}) = \cot (200^{\circ})$

Angles that differ in $270^{\circ}$

Two angles $α$ and $β$ differ in $270^{\circ}$ if, when subtracted, we obtain $270^{\circ}$ : $α - β = 270^{\circ}$ .

Example

An example is the angles of $320^{\circ}$ and $50^{\circ}$ , since $320^{\circ} - 50^{\circ} = 270^{\circ}$ .

When two angles $α$ and $β$ differ in $270^{\circ}$ we have:

$\sin (α) = - \cos (β)$
$\cos (α) = \sin (β)$
$\tan (α) = - \cot (β)$

Example

In our example with the angle of $320^{\circ}$ and $50^{\circ}$ , we have:

$\sin (320^{\circ}) = - \cos (50^{\circ})$
$\cos (320^{\circ}) = \sin (50^{\circ})$
$\tan (320^{\circ}) = - \cot (50^{\circ})$

Supplementary angles

Angles that differ in 180∘

Opposite angles

Negative angles

Angles greater than 360∘

Angles that differ in 90∘

Angles that add up to 270∘

Angles that differ in 270∘

Angles that differ in $180^{\circ}$

Angles greater than $360^{\circ}$

Angles that differ in $90^{\circ}$

Angles that add up to $270^{\circ}$

Angles that differ in $270^{\circ}$