Angles Suplementaris
Dos angles s'anomenen suplementaris si sumen $$180^\circ$$.
$$140^\circ$$ i $$40^\circ$$ són angles suplementaris ja que: $$$140^\circ+ 40^\circ=180^\circ $$$
El sinus, cosinus i tangent dels angles suplementaris tenen certa relació. Si $$\alpha$$ i $$\beta$$ són dos angles suplementaris llavors:
-
$$\sin(\alpha)=\sin(\beta)$$
-
$$\cos(\alpha)=-\cos(\beta)$$
- $$\tan(\alpha)=-\tan(\beta)$$
És a dir, els sinus són iguals, i el cosinus i la tangent canvien de signe.
En l'exemple anterior, doncs, tenim que:
-
$$\sin(40^\circ)=\sin(140^\circ)$$
-
$$\cos(40^\circ)=-\cos(140^\circ)$$
- $$\tan(40^\circ)=-\tan(140^\circ)$$
Angles que es diferencien en $$180^\circ$$
Dos angles $$\alpha$$ i $$\beta$$ es diferencien en $$180^\circ$$ si $$\alpha-\beta=180^\circ$$.
$$240^\circ$$ i $$60^\circ$$ es diferencien en $$180^\circ$$, ja que : $$$240^\circ-60^\circ=180^\circ$$$
El sinus, cosinus i tangent de dos angles que es diferencien en $$180^\circ$$ també estan relacionats. Si $$\alpha$$ i $$\beta$$ es diferencien en $$180^\circ$$, aleshores:
-
$$\sin(\alpha)=-\sin(\beta)$$
-
$$\cos(\alpha)=-\cos(\beta)$$
- $$\tan(\alpha)=\tan(\beta)$$
És a dir, el sinus i el cosinus canvien de signe, però la tangent és la mateixa en els dos angles.
En l'exemple anterior:
-
$$\sin(240^\circ)=-\sin(60^\circ)$$
-
$$\cos(240^\circ)=-\cos(60^\circ)$$
- $$\tan(240^\circ)=\tan(60^\circ)$$
Angles oposats
Dos angles s'anomenen oposats si sumen $$360^\circ$$. És a dir, $$\alpha$$ i $$\beta$$ són oposats si $$\alpha+\beta=360^\circ$$.
$$330^\circ$$ i $$30^\circ$$ són oposats, ja que $$$330^\circ+30^\circ=360^\circ$$$
Els sinus, cosinus i tangents de angles oposats estan relacionats d'una forma similar de com es va veure amb els angles suplementaris o els que es diferencien en $$180^\circ$$. Així, si $$\alpha$$ i $$\beta$$ són angles oposats es compleix sempre que:
-
$$\sin(\alpha)=-\sin(\beta)$$
-
$$\cos(\alpha)=\cos(\beta)$$
- $$\tan(\alpha)=-\tan(\beta)$$
És a dir, el sinus i la tangent són el mateix però amb diferent signe, i el cosinus és exactament el mateix.
En l'exemple anterior es té:
-
$$\sin(330^\circ)=-\sin(30^\circ)$$
-
$$\cos(330^\circ)=\cos(30^\circ)$$
- $$\tan(330^\circ)=-\tan(30^\circ)$$
Angles negatius
Un angle és negatiu si va en direcció contrària a les agulles del rellotge, i es simbolitza amb un menys davant.
Si es fa un angle de $$30^\circ$$, però en comptes d'anar cap amunt es va cap avall, es diu que l'angle és de $$-30^\circ$$.
La següent il·lustració mostra l'angle negatiu $$-30^\circ$$:
Si $$\alpha$$ és un angle, llavors és tenen les següents igualtats:
-
$$\sin(-\alpha)=-\sin(\alpha)$$
-
$$\cos(-\alpha)=\cos(\alpha)$$
- $$\tan(-\alpha)=-\tan(\alpha)$$
En resum, el sinus i la tangent de $$\alpha$$ i $$-\alpha$$ són el mateix però amb diferent signe, i el cosinus és exactament el mateix.
En l'exemple anterior es té:
-
$$\sin(-30^\circ)=-\sin(30^\circ)$$
-
$$\cos(-30^\circ)=\cos(30^\circ)$$
- $$\tan(-30^\circ)=-\tan(30^\circ)$$
Angles majors de $$360^\circ$$
Per calcular el sinus, el cosinus i la tangent de angles grans de $$360^\circ$$, es segueixen els següents passos:
-
Es fa la divisió entera de l'angle entre $$360$$. Per exemple, si l'angle és $$780^\circ$$, es fa:
-
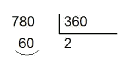
S'agafa el residu. En l'exemple anterior és $$60^\circ$$.
- El sinus, el cosinus i la tangent de l'angle són el del residu que s'ha obtingut.
Tornant a l'exemple anterior, es té:
-
$$\sin(780^\circ)=\sin(660^\circ)$$
-
$$\cos(780^\circ)=\cos(60^\circ)$$
- $$\tan(780^\circ)=\tan(60^\circ)$$
Angles que es diferencien en $$90^\circ$$
Dos angles es diferencien en $$90^\circ$$ si el resultat de restar és $$90^\circ$$.
Per exemple $$160^\circ$$ i $$70^\circ$$, ja que: $$160^\circ- 70^\circ= 90^\circ$$. La següent il·lustració ho mostra més clarament:
Les raons que satisfan dos angles $$\alpha$$ i $$\beta$$ si es diferencien en $$90^\circ$$ (és a dir, si $$\alpha-\beta=90^\circ$$) són:
-
$$\sin(\alpha)=\cos(\beta)$$
-
$$\cos(\alpha)=-\sin(\beta)$$
- $$\tan(\alpha)=-\cot(\beta)$$
En l'exemple anterior es té:
-
$$\sin(160^\circ)=\cos(70^\circ)$$
-
$$\cos(160^\circ)=-\sin(70^\circ)$$
- $$\tan(160^\circ)=-\cot(70^\circ)$$
Angles que sumen $$270^\circ$$
Dos angles $$\alpha$$ i $$\beta$$ sumen $$270^\circ$$ si $$\alpha+\beta=270^\circ$$.
Per exemple $$70^\circ$$ i $$200^\circ$$, ja que $$70^\circ + 200^\circ=270^\circ$$.
En aquest cas, $$\alpha$$ i $$\beta$$ satisfan les següents igualtats:
-
$$\sin(\alpha)=-\cos(\beta)$$
-
$$\cos(\alpha)=-\sin(\beta)$$
- $$\tan(\alpha)=\cot(\beta)$$
En l'exemple anterior, es té:
-
$$\sin(70^\circ)=-\cos(200^\circ)$$
-
$$\cos(70^\circ)=-\sin(200^\circ)$$
- $$\tan(70^\circ)=\cot(200^\circ)$$
Angles que es diferencien en $$270^\circ$$
Dos angles $$\alpha$$ i $$\beta$$ es diferencien en $$270^\circ$$ si a la resta s'obté exactament $$270^\circ$$: $$\alpha-\beta= 270^\circ$$.
Un exemple serien els angles $$320^\circ$$ i $$50^\circ$$, ja que $$320^\circ-50^\circ=270^\circ$$.
Quan dos angles $$\alpha$$ i $$\beta$$ es diferencien en $$270^\circ$$ es compleix que:
-
$$\sin(\alpha)=-\cos(\beta)$$
-
$$\cos(\alpha)=\sin(\beta)$$
- $$\tan(\alpha)=-\cot(\beta)$$
Si ho calculem per als angles $$320^\circ$$ i $$50^\circ$$, tenim:
-
$$\sin(320^\circ)=-\cos(50^\circ)$$
-
$$\cos(320^\circ)=\sin(50^\circ)$$
- $$\tan(320^\circ)=-\cot(50^\circ)$$