Ángulos suplementarios
Dos ángulos se llaman suplementarios si suman $$180^\circ$$.
$$140^\circ$$ y $$40^\circ$$ son ángulos suplementarios ya que: $$$140^\circ+ 40^\circ=180^\circ $$$
El seno, coseno y tangente de los ángulos suplementarios tienen cierta relación. Si $$\alpha$$ y $$\beta$$ son dos ángulos suplementarios entonces se tiene que:
-
$$\sin(\alpha)=\sin(\beta)$$
-
$$\cos(\alpha)=-\cos(\beta)$$
- $$\tan(\alpha)=-\tan(\beta)$$
Es decir, los senos son iguales, y el coseno y la tangente cambian de signo.
En el ejemplo anterior, pues, se tiene que:
-
$$\sin(40^\circ)=\sin(140^\circ)$$
-
$$\cos(40^\circ)=-\cos(140^\circ)$$
- $$\tan(40^\circ)=-\tan(140^\circ)$$
Ángulos que se diferencian en $$180^\circ$$
Dos ángulos $$\alpha$$ y $$\beta$$ se diferencian en $$180^\circ$$ si $$\alpha-\beta=180^\circ$$.
$$240^\circ$$ y $$60^\circ$$ se diferencian en $$180^\circ$$, ya que: $$$240^\circ-60^\circ=180^\circ$$$
El seno, coseno y tangente de dos ángulos que se diferencian en $$180^\circ$$ también están relacionados. Si $$\alpha$$ y $$\beta$$ se diferencian en $$180^\circ$$, entonces:
-
$$\sin(\alpha)=-\sin(\beta)$$
-
$$\cos(\alpha)=-\cos(\beta)$$
- $$\tan(\alpha)=\tan(\beta)$$
Es decir, el seno y el coseno cambian de signo, pero la tangente es la misma en los dos ángulos.
En el ejemplo anterior:
-
$$\sin(240^\circ)=-\sin(60^\circ)$$
-
$$\cos(240^\circ)=-\cos(60^\circ)$$
- $$\tan(240^\circ)=\tan(60^\circ)$$
Ángulos opuestos
Dos ángulos se llaman opuestos si suman $$360^\circ$$. Es decir, $$\alpha$$ y $$\beta$$ son opuestos si $$\alpha+\beta=360^\circ$$.
$$330^\circ$$ y $$30^\circ$$ son opuestos, ya que $$$330^\circ+30^\circ=360^\circ$$$
Los senos, cosenos y tangentes de ángulos opuestos están relacionados de una forma similar de como se vio con los ángulos suplementarios o los que se diferencian en $$180^\circ$$. Así, si $$\alpha$$ y $$\beta$$ son ángulos opuestos se cumple siempre que:
-
$$\sin(\alpha)=-\sin(\beta)$$
-
$$\cos(\alpha)=\cos(\beta)$$
- $$\tan(\alpha)=-\tan(\beta)$$
Es decir, el seno y la tangente son el mismo pero con diferente signo, y el coseno es exactamente el mismo.
En el ejemplo anterior se tiene:
-
$$\sin(330^\circ)=-\sin(30^\circ)$$
-
$$\cos(330^\circ)=\cos(30^\circ)$$
- $$\tan(330^\circ)=-\tan(30^\circ)$$
Ángulos negativos
Un ángulo es negativo si va en dirección contraria a las agujas del reloj, y se simboliza con un menos delante.
Si se hace un ángulo de $$30^\circ$$, pero en vez de ir hacia arriba se va hacia abajo, se dice que el ángulo es de $$-30^\circ$$.
La siguiente ilustración muestra el ángulo negativo $$-30^\circ$$:
Si $$\alpha$$ es un ángulo, entonces se tienen las siguientes igualdades:
-
$$\sin(-\alpha)=-\sin(\alpha)$$
-
$$\cos(-\alpha)=\cos(\alpha)$$
- $$\tan(-\alpha)=-\tan(\alpha)$$
En resumen, el seno y la tangente de $$\alpha$$ y $$-\alpha$$ son el mismo pero con diferente signo, y el coseno es exactamente el mismo.
En el ejemplo anterior se tiene:
-
$$\sin(-30^\circ)=-\sin(30^\circ)$$
-
$$\cos(-30^\circ)=\cos(30^\circ)$$
- $$\tan(-30^\circ)=-\tan(30^\circ)$$
Ángulos mayores de $$360^\circ$$
Para calcular el seno, el coseno y la tangente de ángulos mayores de $$360^\circ$$, se siguen los siguientes pasos:
-
Se hace la división entera del ángulo entre $$360$$. Por ejemplo, si el ángulo es $$780^\circ$$, se hace:
-
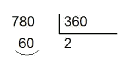
Se coge el residuo. En el ejemplo anterior es $$60^\circ$$.
- El seno, el coseno y la tangente del ángulo son el del residuo que se ha obtenido.
Volviendo al ejemplo anterior, se tiene:
-
$$\sin(780^\circ)=\sin(660^\circ)$$
-
$$\cos(780^\circ)=\cos(60^\circ)$$
- $$\tan(780^\circ)=\tan(60^\circ)$$
Ángulos que se diferencian en $$90^\circ$$
Dos ángulos se diferencian en $$90^\circ$$ si el resultado de restarlos es $$90^\circ$$.
Por ejemplo $$160^\circ$$ y $$70^\circ$$, ya que: $$160^\circ- 70^\circ= 90^\circ$$. La siguiente ilustración lo muestra más claramente:
Las razones que satisfacen dos ángulos $$\alpha$$ y $$\beta$$ si se diferencian en $$90^\circ$$ (es decir, si $$\alpha-\beta=90^\circ$$) son:
-
$$\sin(\alpha)=\cos(\beta)$$
-
$$\cos(\alpha)=-\sin(\beta)$$
- $$\tan(\alpha)=-\cot(\beta)$$
En el ejemplo anterior se tiene:
-
$$\sin(160^\circ)=\cos(70^\circ)$$
-
$$\cos(160^\circ)=-\sin(70^\circ)$$
- $$\tan(160^\circ)=-\cot(70^\circ)$$
Ángulos que suman $$270^\circ$$:
Dos ángulos $$\alpha$$ y $$\beta$$ suman $$270^\circ$$ si $$\alpha+\beta=270^\circ$$.
Por ejemplo $$70^\circ$$ y $$200^\circ$$, ya que $$70^\circ + 200^\circ=270^\circ$$.
En este caso, $$\alpha$$ y $$\beta$$ satisfacen las siguientes igualdades:
-
$$\sin(\alpha)=-\cos(\beta)$$
-
$$\cos(\alpha)=-\sin(\beta)$$
- $$\tan(\alpha)=\cot(\beta)$$
En el ejemplo anterior, se tiene que:
-
$$\sin(70^\circ)=-\cos(200^\circ)$$
-
$$\cos(70^\circ)=-\sin(200^\circ)$$
- $$\tan(70^\circ)=\cot(200^\circ)$$
Ángulos que se diferencian en $$270^\circ$$:
Dos ángulos $$\alpha$$ y $$\beta$$ se diferencian en $$270^\circ$$ si al restarlos se obtiene exactamente $$270^\circ$$: $$\alpha-\beta= 270^\circ$$.
Un ejemplo serían los ángulos $$320^\circ$$ y $$50^\circ$$, ya que $$320^\circ-50^\circ=270^\circ$$.
Cuando dos ángulos $$\alpha$$ y $$\beta$$ se diferencian en $$270^\circ$$ se cumple que:
-
$$\sin(\alpha)=-\cos(\beta)$$
-
$$\cos(\alpha)=\sin(\beta)$$
- $$\tan(\alpha)=-\cot(\beta)$$
Si lo calculamos para los ángulos $$320^\circ$$ y $$50^\circ$$, tenemos que:
-
$$\sin(320^\circ)=-\cos(50^\circ)$$
-
$$\cos(320^\circ)=\sin(50^\circ)$$
- $$\tan(320^\circ)=-\cot(50^\circ)$$