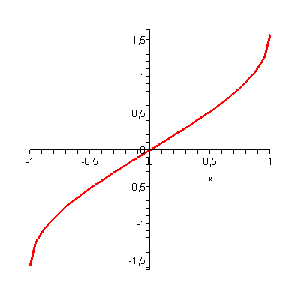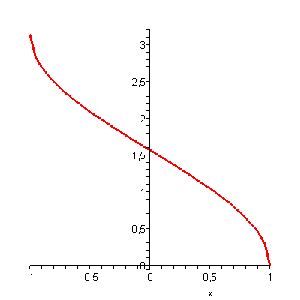En aquesta secció anem a definir les funcions trigonomètriques. En els dos apartats anteriors, hem vist que donat un triangle rectangle $$ABC$$, podem calcular el sinus, el cosinus i la tangent (i les seves funcions inverses respectives), mitjançant el quocient entre dos costats del triangle. En aquest apartat es vol anar un pas més enllà i definir les funcions trigonomètriques. Donat un angle $$x$$, per calcular el seu sinus, per exemple, podem dibuixar un triangle rectangle que un dels dos angles no rectangles sigui $$x$$. Així, un cop dibuixat el triangle, i mitjançant les fórmules donades prèviament, podem calcular el sinus, el cosinus o la tangent. Per tant, com això podem fer-ho per qualsevol angle $$x$$, podem definir una funció per cada valor que se li assigni a $$x$$.
Així, doncs, definim: $$y = sin (x)$$.
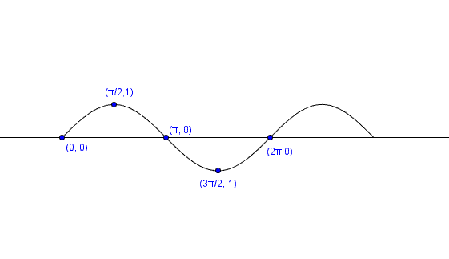
Es diu que $$y$$ és igual al sinus de $$x$$.
La seva funció inversa és: $$x = \arcsin(y)$$
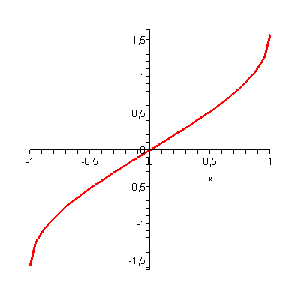
Es diu que $$x$$ és l'arc (de circumferència) quan el sinus val $$y$$, o també, $$x$$ és l'arcsinus de $$y$$.
Si $$y = \cos (x)$$
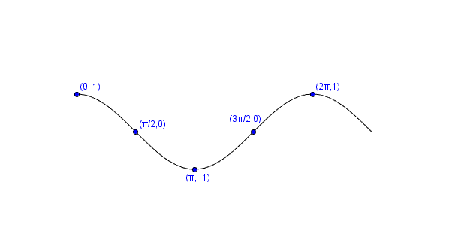
Es diu que $$y$$ és igual al cosinus de $$x$$ i la seva funció inversa és $$x = \arccos(y)$$.
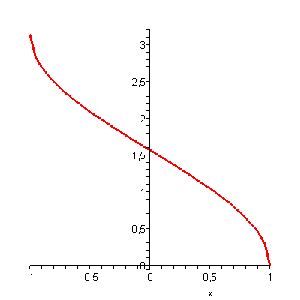
Es diu que $$x$$ és l'arc quan el cosinus val $$y$$, o bé, $$x$$ és el arccosinus de $$y$$.
Si $$y = \tan (x)$$
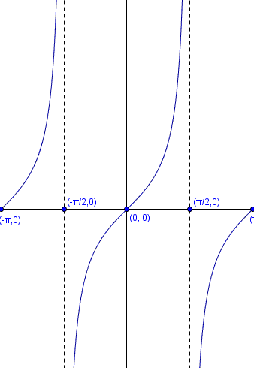
Es diu que $$y$$ és igual a la tangent de $$x$$ i la seva funció inversa és: $$x = \arctan(y)$$.
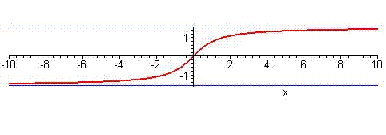
Es diu que $$x$$ és l'arc la tangent del qual val $$y$$, o bé que $$x$$ és igual a l'arctangent de $$y$$.
Noteu, que els valors de $$x$$ poden estar expressats tant en radiants com en graus.