En esta sección vamos a definir las funciones trigonométricas. En los dos apartados anteriores, hemos visto que dado un triangulo rectángulo $$ABC$$, podemos calcular el seno, el coseno y la tangente (y sus funciones inversas respectivas), mediante el cociente entre dos lados del triángulo. En este apartado se quiere ir un paso más allá y definir las funciones trigonométricas. Dado un ángulo $$x$$, para calcular su seno, por ejemplo, podemos dibujar un triángulo rectángulo que uno de los dos ángulos no rectangulos sea $$x$$. Así, una vez dibujado el triangulo, y mediante las fórmulas dadas previamente, podemos calcular el seno, el coseno o la tangente. Por lo tanto, como esto podemos hacerlo por cualquier ángulo $$x$$, podemos definir una función por cada valor que se le asigne a $$x$$.
Así, pues, definimos: $$y = sin (x)$$.
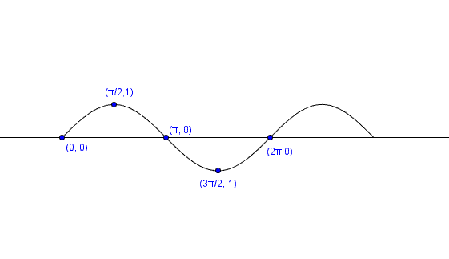
Se dice que $$y$$ es igual al seno de $$x$$.
Su función inversa es: $$x = \arcsin(y)$$
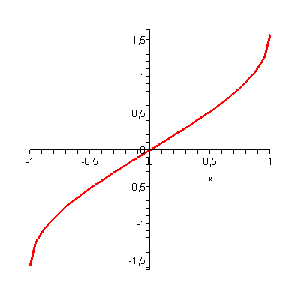
Se dice que $$x$$ es el arco (de circunferencia) cuyo seno vale $$y$$, o también, $$x$$ es el arcoseno de $$y$$.
Si $$y = \cos (x)$$
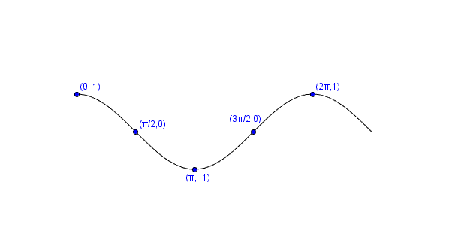
Se dice que $$y$$ es igual al coseno de $$x$$ y su función inversa es $$x = \arccos(y)$$.
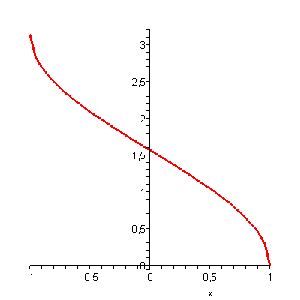
Se dice que $$x$$ es el arco cuyo coseno vale $$y$$, que se dice: $$x$$ es el arcocoseno de $$y$$.
Si $$y = \tan (x)$$
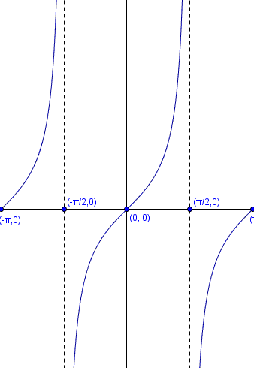
Se dice que $$y$$ es igual a la tangente de $$x$$ y su función inversa es: $$x = \arctan(y)$$.
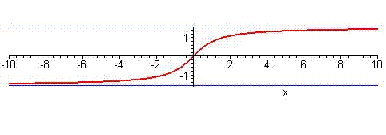
Se dice que $$x$$ es el arco cuya tangente vale $$y$$, o que $$x$$ es igual al arcotangente de $$y$$.
Noteu, que els valors de $$x$$ poden estar expressats tant en radiants com en graus.
