A continuació s'explicarà com trobar els costats i els angles d'un triangle rectangle si només es coneixen alguns d'ells.
En els següents dibuixos, els costats i angles de color vermell són els que no coneixem, mentre els que són negres sí.
Anem a distingir entre els següents casos, depenent dels elements del triangle que es coneixen:
-
Es coneixen la hipotenusa i un catet: En aquest cas s'ha de trobar l'altre catet (el costat $$c$$) i els dos angles aguts (és a dir, $$B$$ i $$C$$).

- L'angle $$B$$ és: $$B=\arcsin\Big( \dfrac{b}{a} \Big)$$
- L'angle $$C$$ és: $$C=90^\circ -B$$
- El costat $$c$$ és: $$c=a\cdot \cos(B)$$
-
Es coneixen dos catets: En aquest cas s'ha de trobar els dos angles aguts ($$B$$ i $$C$$) i la hipotenusa (és a dir, el costat $$a$$).
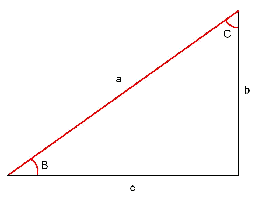
- L'angle $$B$$ és: $$B=\arctan\Big( \dfrac{b}{c}\Big)$$
- L'angle $$C$$ és: $$C=90^\circ - B$$
-
La hipotenusa és: $$a=\dfrac{b}{\sin(B)}$$
També es pot calcular mitjançant la igualtat: $$a=\sqrt{b^2+c^2}$$
-
Es coneixen la hipotenusa i un angle agut: En aquest cas s'haurà de trobar l'altre angle agut (és a dir, $$C$$) i els dos catets (els costats $$b$$ i $$c$$).
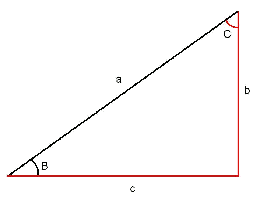
- L'angle $$C$$ és: $$C=90^\circ -B$$
- El costat $$b$$ és: $$b=a\cdot\sin(B)$$
-
El costat $$c$$ és: $$c=a\cos(B)$$
També es pot calcular fent: $$c=\sqrt{a^2+b^2}$$
-
Es coneixen un catet i un angle agut: Aquí s'haurà de calcular l'altre angle agut (com abans, $$C$$), la hipotenusa (el costat $$a$$) i l'altre catet (el costat $$c$$).
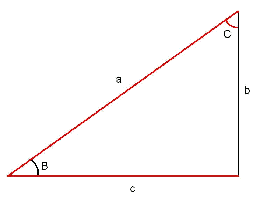
- L'angle $$C$$ és: $$C=90^\circ -B$$
- El costat $$a$$ és: $$a=\dfrac{b}{\sin(B)}$$
-
El costat $$c$$ és: $$c=\dfrac{b}{\tan(B)}$$
També: $$c=\sqrt{a^2+b^2}$$
