A continuación se explicará como hallar los lados y los ángulos de un triángulo rectángulo, si sólo se conocen algunos de ellos.
En los siguientes dibujos, los lados y ángulos de color rojo son los que no se conocen, mientras los que son negros sí.
Vamos a distinguir entre los siguientes casos, dependiendo de los elementos del triángulo que se conocen:
-
Se conocen la hipotenusa y un cateto: En este caso se debe encontrar el otro cateto (el lado

- El ángulo
- El ángulo
- El lado
- El ángulo
-
Se conocen dos catetos: En este caso se tiene que encontrar los dos ángulos agudos (
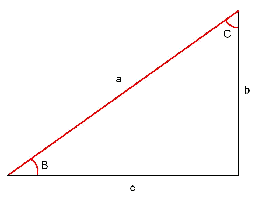
- El ángulo
- El ángulo
-
La hipotenusa es:
También se puede calcular mediante la igualdad:
- El ángulo
-
Se conocen la hipotenusa y un ángulo agudo: En este caso se deberá hallar el otro ángulo agudo (es decir,
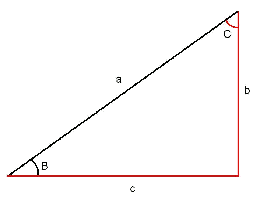
- El ángulo
- El lado
-
El lado
También se puede calcular haciendo:
- El ángulo
-
Se conocen un cateto y un ángulo agudo: Aquí se deberá calcular el otro ángulo agudo (como antes,
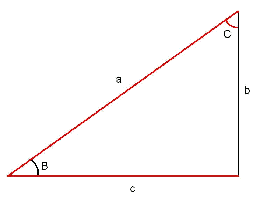
- El ángulo
- El lado
-
El lado
También:
- El ángulo
