Una herramienta muy potente en el cálculo integral es el teorema de Green. Consideremos un campo vectorial $$F(x,y)=(P(x,y),Q(x,y))$$, $$C$$ una curva cerrada en el plano y $$S$$ la superficie interior delimitada por la curva.
Entonces: $$$\int_C F \ dr=\iint_S\big( Q_x-P_y \big) \ dx \ dy$$$
La aplicación en el cálculo de áreas es el siguiente, considerar un campo tal que $$Q_x-P_y=1$$. Entonces el término de la derecha no es más que el área del recinto $$S$$. Por lo tanto, podremos calcularla haciendo una integral de línea en la frontera del recinto.
De campos que cumplan la propiedad $$Q_x-P_y=1$$ hay muchos, pero los más utilizados son:
- $$F(x,y)=(0,x)$$
- $$F(x,y)=(-y,0)$$
- $$F(x,y)=(-y,x)$$
Por ejemplo vamos a calcular el área delimitada por la curva parametrizada por: $$$\alpha(\theta)=(3\sin(2\theta)\cdot\cos(\theta),3\sin(2\theta)\cdot\sin(\theta))$$$
con $$\theta\in\big[0,\dfrac{\pi}{2}\big]$$.
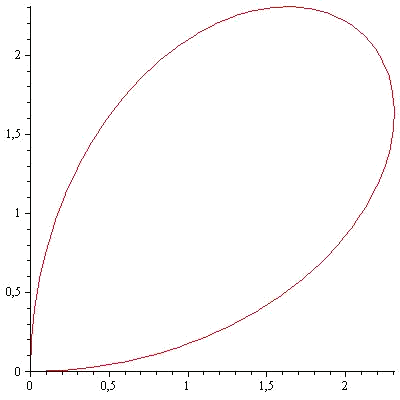
Ahora tomamos el campo vectorial $$F(x,y)=(0,x)$$ e integramos el campo a lo largo de la curva $$\alpha(\theta)$$. Calculemos, pues: $$$ \alpha'(\theta)=(6\cos(2\theta)\cdot\cos(\theta)-3\sin(2\theta)\cdot\sin(\theta),6\cos(2\theta)\cdot\sin(\theta)-3\sin(2\theta)\cdot\cos(\theta))$$$
y tenemos:
$$$ \begin{array}{rl} \text{Área}=& \iint_D 1 \ dx \ dy=\int_C F \ dr = \int_0^{\frac{\pi}{2}} F(\alpha(t))\cdot\alpha'(t) \ dt \\ =& \int_0^{\frac{\pi}{2}} (0,3\sin(2t)\cdot\sin(t)) \cdot (6\cos(2t)\cdot\cos(t)-3\sin(2t)\cdot\sin(t), \\ & \quad \quad \quad \quad 6\cos(2t)\cdot\sin(t)-3\sin(2t)\cdot\cos(t)) \ dt \\ =& \int_0^{\frac{\pi}{2}} 3\sin(2t)\cos(t)\cdot (6\cos(2t)\cdot\sin(t)-3\sin(2t)\cdot\cos(t)) \ dt \\ = & 18\int_0^{\frac{\pi}{2}} \cos(t)\cos(2t)\sin(t)\sin(2t) \ dt + 9\int_0^{\frac{\pi}{2}} \sin^2(2t)\cos^2(2t) \ dt \\ =& 9\int_0^{\frac{\pi}{2}} \sin^2(2t)\cos(2t) \ dt + 9\int_0^{\frac{\pi}{2}} \sin^2(2t)\Big(\dfrac{1+\cos^2(2t)}{2}\Big) \ dt \\ =& \dfrac{9}{2}\Big[\dfrac{sin^3(2t)}{3})\Big]_0^{\frac{\pi}{2}}+ \dfrac{9}{2}\int_0^{\frac{\pi}{2}} \dfrac{1-\cos(4t)}{2} \ dt +\dfrac{9}{2}\int_0^{\frac{\pi}{2}} \sin^2(2t)\cos(2t) \ dt \\ =& \dfrac{9}{8}\cdot\pi \end{array}$$$